
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ994 –Η–Ζ 1087 |
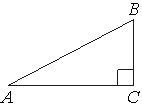 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C ―Ä–Α–≤–Β–Ϋ 90¬Α, BC=3, AB=5. –ù–Α–Ι–¥–Η―²–Β cosB.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C ―Ä–Α–≤–Β–Ϋ 90¬Α, BC=3, AB=5. –ù–Α–Ι–¥–Η―²–Β cosB.
–ü–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é –Κ–Ψ―¹–Η–Ϋ―É―¹–Α:
cosB=BC/AB=3/5=0,6
–û―²–≤–Β―²: 0,6
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –ü–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ―Ä–Α–≤–Ϋ–Α 60, –Α –¥–≤–Β –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―Ä–Α–≤–Ϋ―΄ 4 –Η 20. –ù–Α–Ι–¥–Η―²–Β –Β–≥–Ψ –≤―΄―¹–Ψ―²―΄. –£ –Ψ―²–≤–Β―²–Β ―É–Κ–Α–Ε–Η―²–Β –±–Ψ–Μ―¨―à―É―é –≤―΄―¹–Ψ―²―É.
–ü–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ―Ä–Α–≤–Ϋ–Α 60, –Α –¥–≤–Β –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―Ä–Α–≤–Ϋ―΄ 4 –Η 20. –ù–Α–Ι–¥–Η―²–Β –Β–≥–Ψ –≤―΄―¹–Ψ―²―΄. –£ –Ψ―²–≤–Β―²–Β ―É–Κ–Α–Ε–Η―²–Β –±–Ψ–Μ―¨―à―É―é –≤―΄―¹–Ψ―²―É.
 –€–Β–¥–Η–Α–Ϋ–Α BM –Η –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α AP ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β K, –¥–Μ–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AC –Ψ―²–Ϋ–Ψ―¹–Η―²―¹―è –Κ –¥–Μ–Η–Ϋ–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Κ–Α–Κ 6:5. –ù–Α–Ι–¥–Η―²–Β –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –Ω–Μ–Ψ―â–Α–¥–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α AKM –Κ –Ω–Μ–Ψ―â–Α–¥–Η ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α KPCM.
–€–Β–¥–Η–Α–Ϋ–Α BM –Η –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α AP ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β K, –¥–Μ–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AC –Ψ―²–Ϋ–Ψ―¹–Η―²―¹―è –Κ –¥–Μ–Η–Ϋ–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Κ–Α–Κ 6:5. –ù–Α–Ι–¥–Η―²–Β –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –Ω–Μ–Ψ―â–Α–¥–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α AKM –Κ –Ω–Μ–Ψ―â–Α–¥–Η ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α KPCM.
 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C ―Ä–Α–≤–Β–Ϋ 90¬Α, cosB=5/6, AB=18. –ù–Α–Ι–¥–Η―²–Β BC.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C ―Ä–Α–≤–Β–Ϋ 90¬Α, cosB=5/6, AB=18. –ù–Α–Ι–¥–Η―²–Β BC.
 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η 16 –Η 2 –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –≤―΄―¹–Ψ―²―΄ –Κ ―ç―²–Η–Φ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ. –£―΄―¹–Ψ―²–Α, –Ω―Ä–Ψ–≤–Β–¥―ë–Ϋ–Ϋ–Α―è –Κ –Ω–Β―Ä–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Β, ―Ä–Α–≤–Ϋ–Α 1. –ß–Β–Φ―É ―Ä–Α–≤–Ϋ–Α –≤―΄―¹–Ψ―²–Α, –Ω―Ä–Ψ–≤–Β–¥―ë–Ϋ–Ϋ–Α―è –Κ–Ψ –≤―²–Ψ―Ä–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Β?
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η 16 –Η 2 –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –≤―΄―¹–Ψ―²―΄ –Κ ―ç―²–Η–Φ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ. –£―΄―¹–Ψ―²–Α, –Ω―Ä–Ψ–≤–Β–¥―ë–Ϋ–Ϋ–Α―è –Κ –Ω–Β―Ä–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Β, ―Ä–Α–≤–Ϋ–Α 1. –ß–Β–Φ―É ―Ä–Α–≤–Ϋ–Α –≤―΄―¹–Ψ―²–Α, –Ω―Ä–Ψ–≤–Β–¥―ë–Ϋ–Ϋ–Α―è –Κ–Ψ –≤―²–Ψ―Ä–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Β?
 –ü―Ä―è–Φ–Α―è, –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Β AC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η BC –≤ ―²–Ψ―΅–Κ–Α―Ö M –Η N ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ, AC=21, MN=14. –ü–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC ―Ä–Α–≤–Ϋ–Α 27. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α MBN.
–ü―Ä―è–Φ–Α―è, –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Β AC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η BC –≤ ―²–Ψ―΅–Κ–Α―Ö M –Η N ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ, AC=21, MN=14. –ü–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC ―Ä–Α–≤–Ϋ–Α 27. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α MBN.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: