
 Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
Средняя линия трапеции равна полусумме оснований и не зависит от высоты:
m=(11+19)/2=30/2=15
Ответ: 15
Поделитесь решением
Присоединяйтесь к нам...
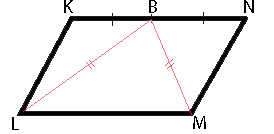 В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
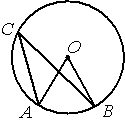 Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
Синус острого угла A треугольника ABC равен 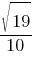 . Найдите CosA.
. Найдите CosA.
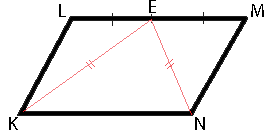 В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
 Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Комментарии: