Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.
2) Существует параллелограмм, который не является прямоугольником.
3) Сумма углов тупоугольного треугольника равна 180°.
Рассмотрим каждое утверждение:
1) "Центры
вписанной и описанной окружностей
равнобедренного треугольника совпадают." - это утверждение неверно, т.к. центр вписанной окружности находится внутри треугольника, а центр описанной окружности может находиться вне треугольника (по
теореме об окружности).
2) "Существует
параллелограмм, который не является
прямоугольником." - это утверждение верно, т.к. не противоречит
определению параллелограмма.
3) "Сумма углов
тупоугольного треугольника равна 180°." - это утверждение верно, т.к. не противоречит
теореме о сумме углов треугольника.
Поделитесь решением
Присоединяйтесь к нам...
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
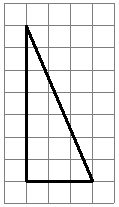На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Найдите угол ABC . Ответ дайте в градусах.
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 14°?
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: