
Решите неравенство x2-36>0.
1) (-∞;+∞)
2) (-∞;-6)∪(6;+∞)
3) (-6;6)
4) нет решений
Для решения неравенства найдем корни
квадратного уравнения x2-36=0.
(x-6)(x+6)=0
Произведение равно нулю, когда один из множителей равен нулю, тогда:
1) x-6=0
x1=6
2) x+6=0
x2=-6
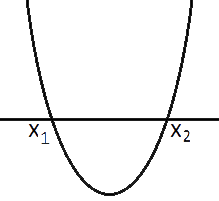 График квадратичной функции - парабола.
График квадратичной функции - парабола.
Аргумент "а" равен 1, т.е. больше нуля, значит ветви параболы направлены вверх. Корни уравнения - точки пересечения графика функции оси Х.
Значение функции больше нуля в диапазонах, где график располагается выше оси Х, в данном случае (-∞;-6) и (6;+∞).
Ответ: 2)
Поделитесь решением
Присоединяйтесь к нам...
Решите систему уравнений 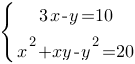
Первую половину трассы автомобиль проехал со скоростью 84 км/ч, а вторую — со скоростью 96 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решите уравнение 1-5x=-6x+8.
В начале года число абонентов телефонной компании «Восток» составляло 500 тыс. человек, а в конце года их стало 575 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
Решите уравнение (x+2)(-x+6)=0.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Комментарии:
(2017-04-26 18:51:00) Администратор: Елена, √25*6-√6=5√6-√6=4√6
(2017-04-25 15:38:48) Елена: √150-√6
(2016-10-27 21:19:24) Администратор: irina, это обычное квадратное уравнение, решается через дискриминант.
(2016-10-26 15:58:42) irina: 3x^2+x√7-2=0