
 Стороны AC, AB, BC треугольника ABC равны 2√
Стороны AC, AB, BC треугольника ABC равны 2√
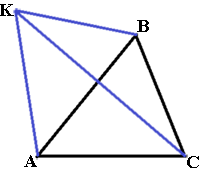
По условию задачи ∠KAC>90°, т.е. это наибольший угол в треугольнике AKC следовательно, сторона KC, противолежащая этому углу тоже наибольшая (по теореме о соотношениях между сторонами и углами треугольника).
Сторона AC равная 2√
Следовательно, угол ABC - наибольший угол треугольника ABC.
По условию задачи треугольник KAC подобен исходному треугольнику ABC. А значит углы этих треугольников соответственно равны (по определению подобных треугольников).
Поэтому наибольшие углы двух рассматриваемых треугольников равны, т.е. ∠KAC=∠ABC.
∠ACK не равен ∠ACB (т.к. KC пересекает сторону AB в точке, отличной от B), поэтому ∠ACK = ∠BAC.
Следовательно, ∠AKC=∠ACB => cos(∠AKC)=cos(∠ACB).
Применяя теорему косинусов, мы можем записать:
AB2=AC2+BC2-2*AC*BC*cos(∠ACB).
(√
11=4*5+4-8*√
11-24=-8*√
13=8*√
cos(∠AKC)=cos(∠ACB)=13/(8*√
Ответ: 13/(8*√
Поделитесь решением
Присоединяйтесь к нам...
 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.
 В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
Какое наибольшее число коробок в форме прямоугольного параллелепипеда размером 30Х40Х50 (см) можно поместить в кузов машины размером 3Х2Х3,5 (м)?
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 80°. Найдите величину угла OAB.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 80°. Найдите величину угла OAB.
Стороны AC, AB, BC треугольника ABC равны 2√
Комментарии:
(2019-06-03 21:39:23) Администратор: Гоша, конечно можно, а нужно?
(2019-06-02 15:43:22) гоша: Можно избавиться от иррациональности в знаменателе. 13*sqrt(5)/8*sqrt(5)*sqrt(5)=13*sqrt(5)/8*5
(2019-04-29 19:09:21) Администратор: Даниил, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2019-04-23 15:20:12) Даниил: точька о-центор окружнасти на которай лежат точька а.в и с. Известно,ЧТО УГОЛА АВС =69 , И УГОЛ ОАВ=48. Найти уголвсо. Ответдайте в градусах
(2017-05-28 23:22:17) Администратор: Alissa, посмотрите на рисунок. У этих треугольников нет общих углов. А равенство углов объясняется в решении.
(2017-05-21 08:34:49) Alissa: Мне непонятно,почему у треугольников КАС и АВС равны углы КАС и АВС???. Ведь у них общий угол А?
(2015-05-26 18:10:32) Мария: Администраторы, спасибо Вам огромное!!!! Невероятно удобный сайт!
(2015-04-19 11:26:31) Администратор: Алина, к сожалению, у меня нет такой информации.
(2015-04-19 08:58:19) Алина: Это вторая часть?
(2015-04-12 14:26:36) Таня: Спасибо за сайт, отличная помощь при подготовке к экзамену
(2015-04-09 21:09:07) Аделя: Огромное спасибо за этот сайт! Я безмерно благодарна:)
(2015-03-24 14:12:35) Любовь: А это задание в гиа под каким номером?
(2015-03-21 13:26:28) sen: Замечательный сайт
(2015-03-04 20:56:03) Администратор: Диана, спасибо большое за такой отзыв, очень приятно читать!!! А Вам успехов на экзаменах.
(2015-03-04 20:52:57) Диана: Ну,я могу добавить ко всем выше сказанным словам,с которыми я полностью согласна, что ваш сайт ,действительно, очень хороший. Разбираете нам такие задачи,о которых лично я не задумывалась,а теперь стала понимать, и у меня стало всё получаться( тьфу,тьфу тьфу). Вам за это огромное спасибо. Обожаю ваш сайт.
(2014-12-23 11:49:06) Администратор: Таня, и Вам спасибо за теплые слова, очень радостно, что наш труд не напрасен и приносит реальную пользу. Удачи, а главное Успехов в учебе!
(2014-12-23 11:28:34) Таня: Даже удивительно, что в наше время существует сайт, который бесплатно помогает в подготовке к экзаменам. Большое спасибо разработчикам и авторам! Вы такую работу делаете ! Счастья Вам , успехов во всем.
(2014-11-28 02:23:06) Балобина Егор: Спасибо за замечательный сайт! Здоровья Вам!
(2014-11-05 20:55:03) Мария: Спасибо за помощь. Удачи по жизни
(2014-05-29 21:25:30) Лена : Спасибо огромное за этот замечательный сайт!