Какое наибольшее число коробок в форме прямоугольного параллелепипеда размером 30Х40Х50 (см) можно поместить в кузов машины размером 3Х2Х3,5 (м)?
Посчитаем объем кузова в м3:
3*2*3,5=21 м3.
Посчитаем объем одной коробки в м3, размеры коробки даны в сантиметрах - надо перевести в метры:
30Х40Х50 (см) = 0,3Х0,4Х0,5 (м), следовательно объем одной коробки:
0,3*0,4*0,5=0,06 м3
Разделим объем кузова на объем коробки:
21/0,06=350
Ответ: 350
Поделитесь решением
Присоединяйтесь к нам...
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=21, AO=75.
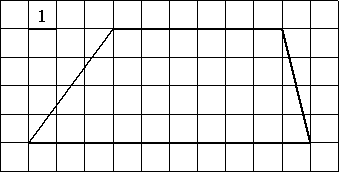Найдите площадь трапеции, изображённой на рисунке.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=21, MN=14. Площадь треугольника ABC равна 27. Найдите площадь треугольника MBN.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
Синус острого угла A треугольника ABC равен 
. Найдите CosA.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-09-18 14:34:01) Администратор: Татьяна, я думал об этом. Если рассматривать Ваш вариант, то надо проверять все варианты укладки коробок (вертикально, горизонтально, на боку, вдоль одной стенки, вдоль другой и т.д.) и определять, при каком из них можно впихнуть максимальное количество коробок. А если учесть, что есть варианты, когда каждая коробка укладывается в свое положение (как в тетрисе), то задача становится нерешаемой.
Поэтому я подумал, так как не требуется указывать способ укладки, то достаточно понять теоретически, сколько коробок поместится в данном объеме.
(2019-09-18 09:51:27) Татьяна: Почему вы не рассматриваете , что коробка имеет вполне контрентые объемы ? и зазор залить своим объемом она не сможет( Разве не нужно делить все параметры кузова на параметры коробки?