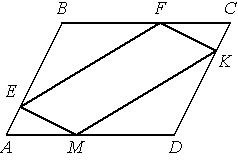
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Рассмотрим треугольники АЕМ и CKF.
АЕ = CK (по условию задачи)
/A=/C (по
свойству параллелограмма)
Т.к. AD=BC (по
свойству параллелограмма), а BF = DM (по условию), то АМ=CF.
Следовательно, треугольники АЕМ и CKF равны (по первому признаку).
Поэтому ЕМ=FK.
Аналогично доказывается, что треугольники EBF и KDM тоже равны, следовательно EF=MK.
Т.е. противоположные стороны данного четырехугольника равны. Соответственно этот четырехугольник - параллелограмм (по
свойству параллелограмма).
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Какой угол (в градусах) описывает часовая стрелка за 2 часа 16 минут?
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=7.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-06-08 11:28:24) Администратор: Света, прямоугольник - это тоже параллелограмм.
(2015-05-26 13:34:16) Света: Но ведь у прямоугольника противолежащие стороны тоже равны.
(2015-05-26 13:33:41) Света: Но ведь у прямоугольника противолежащие стороны тоже равны.
(2015-05-23 20:47:28) Администратор: Малина, а то, что противоположные стороны взаимно равны - доказывает.
(2015-05-23 20:41:29) Малина: То, что треугольники равны, не доказывает, что EFKM параллелограмм