
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ30 –Η–Ζ 1087 |
 –‰–Ζ ―²–Ψ―΅–Κ–Η –ê –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–≤–Β –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Β –Κ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β –û. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η –ê –¥–Ψ ―²–Ψ―΅–Κ–Η –û, –Β―¹–Μ–Η ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Φ–Η ―Ä–Α–≤–Β–Ϋ 60¬Α, –Α ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 8.
–‰–Ζ ―²–Ψ―΅–Κ–Η –ê –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–≤–Β –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Β –Κ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β –û. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η –ê –¥–Ψ ―²–Ψ―΅–Κ–Η –û, –Β―¹–Μ–Η ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Φ–Η ―Ä–Α–≤–Β–Ϋ 60¬Α, –Α ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 8.
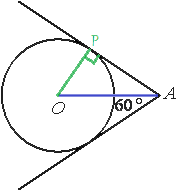 –ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ –ê–û.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ –ê–û.
–û–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ –Ψ–¥–Ϋ―É –Η–Ζ ―²–Ψ―΅–Β–Κ –Κ–Α―¹–Α–Ϋ–Η―è –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Η –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι –Κ–Α–Κ –†.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ –û–†.
–û–† ―è–≤–Μ―è–Β―²―¹―è ―Ä–Α–¥–Η―É―¹–Ψ–Φ –Η –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ψ–Φ –Κ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι –ê–† (–Ω–Ψ ―¹–≤–Ψ–Ι―¹―²–≤―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι).
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ –ê–û–†.
–î–Α–Ϋ–Ϋ―΄–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ―è–≤–Μ―è–Β―²―¹―è –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Φ,―².–Κ. –û–† –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Β–Ϋ –ê–†.
–ê–û ―è–≤–Μ―è–Β―²―¹―è –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Ψ–Ι ―É–≥–Μ–Α, –Ψ–±―Ä–Α–Ζ–Ψ–≤–Α–Ϋ–Ϋ–Ψ–≥–Ψ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Φ–Η (―¹–≤–Ψ–Ι―¹―²–≤–Ψ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄―Ö –Ω―Ä―è–Φ―΄―Ö). –Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, ―É–≥–Ψ–Μ –†–ê–û ―Ä–Α–≤–Β–Ϋ –Ω–Ψ–Μ–Ψ–≤–Η–Ϋ–Β –¥–Α–Ϋ–Ϋ–Ψ–≥–Ψ ―É–≥–Μ–Α, ―².–Β. 30¬Α.
sinPAO=OP/AO (–Ω–Ψ –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é ―¹–Η–Ϋ―É―¹–Α).
sin30¬Α=8/AO
1/2=8/AO (–Ω–Ψ ―²–Α–±–Μ–Η―Ü–Β ―¹–Η–Ϋ―É―¹–Ψ–≤)
1=2*8/AO
AO=16
–û―²–≤–Β―²: 16
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
–ö–Α–Κ–Η–Β –Η–Ζ –¥–Α–Ϋ–Ϋ―΄―Ö ―É―²–≤–Β―Ä–Ε–¥–Β–Ϋ–Η–Ι –≤–Β―Ä–Ϋ―΄? –½–Α–Ω–Η―à–Η―²–Β –Η―Ö –Ϋ–Ψ–Φ–Β―Ä–Α.
1) –£–Ψ–Κ―Ä―É–≥ –Μ―é–±–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –Φ–Ψ–Ε–Ϋ–Ψ –Ψ–Ω–Η―¹–Α―²―¨ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨.
2) –ï―¹–Μ–Η –Ω―Ä–Η –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η–Η –¥–≤―É―Ö –Ω―Ä―è–Φ―΄―Ö ―²―Ä–Β―²―¨–Β–Ι –Ω―Ä―è–Φ–Ψ–Ι ―¹―É–Φ–Φ–Α –≤–Ϋ―É―²―Ä–Β–Ϋ–Ϋ–Η―Ö –Ψ–¥–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Η―Ö ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Ϋ–Α
180¬Α, ―²–Ψ ―ç―²–Η –Ω―Ä―è–Φ―΄–Β –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄.
3) –ü–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –Ϋ–Β –Ω―Ä–Β–≤―΄―à–Α–Β―² –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η―è –¥–≤―É―Ö –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ.
 –û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η AC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –≤ ―²–Ψ―΅–Κ–Α―Ö K –Η P ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ –Η –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ –≤–Β―Ä―à–Η–Ϋ―΄ B –Η C. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É –Ψ―²―Ä–Β–Ζ–Κ–Α KP, –Β―¹–Μ–Η AP=18, –Α ―¹―²–Ψ―Ä–Ψ–Ϋ–Α BC –≤ 1,2 ―Ä–Α–Ζ–Α –Φ–Β–Ϋ―¨―à–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB.
–û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η AC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –≤ ―²–Ψ―΅–Κ–Α―Ö K –Η P ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ –Η –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ –≤–Β―Ä―à–Η–Ϋ―΄ B –Η C. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É –Ψ―²―Ä–Β–Ζ–Κ–Α KP, –Β―¹–Μ–Η AP=18, –Α ―¹―²–Ψ―Ä–Ψ–Ϋ–Α BC –≤ 1,2 ―Ä–Α–Ζ–Α –Φ–Β–Ϋ―¨―à–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB.
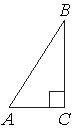 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C ―Ä–Α–≤–Β–Ϋ 90¬Α, sinB=3/5, AB=10. –ù–Α–Ι–¥–Η―²–Β AC.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C ―Ä–Α–≤–Β–Ϋ 90¬Α, sinB=3/5, AB=10. –ù–Α–Ι–¥–Η―²–Β AC.
 –Γ―²–Ψ―Ä–Ψ–Ϋ–Α –Κ–≤–Α–¥―Ä–Α―²–Α ―Ä–Α–≤–Ϋ–Α 6√3. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―ç―²–Ψ–≥–Ψ –Κ–≤–Α–¥―Ä–Α―²–Α.
–Γ―²–Ψ―Ä–Ψ–Ϋ–Α –Κ–≤–Α–¥―Ä–Α―²–Α ―Ä–Α–≤–Ϋ–Α 6√3. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―ç―²–Ψ–≥–Ψ –Κ–≤–Α–¥―Ä–Α―²–Α.
 –£―΄―¹–Ψ―²–Α BH ―Ä–Ψ–Φ–±–Α ABCD –¥–Β–Μ–Η―² –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ―É AD –Ϋ–Α –Ψ―²―Ä–Β–Ζ–Κ–Η AH=21 –Η HD=54. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Ψ–Φ–±–Α.
–£―΄―¹–Ψ―²–Α BH ―Ä–Ψ–Φ–±–Α ABCD –¥–Β–Μ–Η―² –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ―É AD –Ϋ–Α –Ψ―²―Ä–Β–Ζ–Κ–Η AH=21 –Η HD=54. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Ψ–Φ–±–Α.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2019-01-26 16:56:06) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –î–Α–Ϋ–Η–Μ–Α, ―è ―Ä–Α―¹–Ω–Η―¹–Α–Μ ―Ä–Β―à–Β–Ϋ–Η–Β –Ϋ–Β–Φ–Ϋ–Ψ–≥–Ψ –Ω–Ψ–¥―Ä–Ψ–±–Ϋ–Β–Ι, –Ϋ–Α–¥–Β―é―¹―¨, ―¹―²–Α–Μ–Ψ –Ω–Ψ–Ϋ―è―²–Ϋ–Β–Ι. –ï―¹–Μ–Η –Ϋ–Β―², –Ω–Η―à–Η―²–Β.
(2019-01-25 16:13:14) –î–Α–Ϋ–Η–Μ–Α: –‰ –Ω–Ψ―΅–Β–Φ―É –Φ―΄ –≤–Ζ―è–Μ–Η –Η–Φ–Β–Ϋ–Ϋ–Ψ –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β ―¹–Η–Ϋ―É―¹–Α?
(2019-01-25 15:51:47) –î–Α–Ϋ–Η–Μ–Α: –û―²–Κ―É–¥–Α –≤–Ζ―è―²–Ψ 2?
(2016-12-05 22:33:33) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –Κ–Α―²―è, –Ω–Ψ―¹–Φ–Ψ―²―Ä–Η―²–Β –Ζ–Α–¥–Α―΅―É 101 –Η–Ζ ―Ä–Α–Ζ–¥–Β–Μ–Α "–Γ―²–Α―²–Η―¹―²–Η–Κ–Α –Η ―²–Β–Ψ―Ä–Η―è –≤–Β―Ä–Ψ―è―²–Ϋ–Ψ―¹―²–Β–Ι", –Ψ―΅–Β–Ϋ―¨ –Ω–Ψ―Ö–Ψ–Ε–Α –Ϋ–Α –£–Α―à―É.
(2016-12-05 17:26:10) –Κ–Α―²―è: –£ ―¹―Ä–Β–¥–Ϋ–Β–Φ –Ϋ–Α 50 –Κ–Α―Ä–Φ–Α–Ϋ–Ϋ―΄―Ö ―³–Ψ–Ϋ–Α―Ä–Η–Κ–Ψ–≤, –Ω–Ψ―¹―²―É–Ω–Η–≤―à–Η―Ö –≤ –Ω―Ä–Ψ–¥–Α–Ε―É, –Ω―Ä–Η―Ö–Ψ–¥–Η―²―¹―è –≤–Ψ―¹–Β–Φ―¨ –Ϋ–Β–Η―¹–Ω―Ä–Α–≤–Ϋ―΄―Ö. –ù–Α–Ι–¥–Η―²–Β –≤–Β―Ä–Ψ―è―²–Ϋ–Ψ―¹―²―¨ ―²–Ψ–≥–Ψ, ―΅―²–Ψ –≤―΄–±―Ä–Α–Ϋ–Ϋ―΄–Ι –Ϋ–Α―É–¥–Α―΅―É –≤ –Φ–Α–≥–Α–Ζ–Η–Ϋ–Β ―³–Ψ–Ϋ–Α―Ä–Η–Κ –Ψ–Κ–Α–Ε–Β―²―¹―è –Η―¹–Ω―Ä–Α–≤–Β–Ϋ