
 Сторона квадрата равна 6√3. Найдите площадь этого квадрата.
Сторона квадрата равна 6√3. Найдите площадь этого квадрата.
Площадь квадрата:
S = a2 = (6√3)2 = 62*(√3)2 = 36*3 = 108
Ответ: 108
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 6 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 9:7. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 9:7. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
 Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
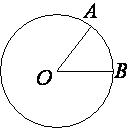 На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
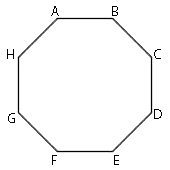 ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
Комментарии: