
 Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
По
первому свойству квадрата, все его углы прямые, следовательно, треугольники, которые образует диагональ, прямоугольные.
Т.е. к этим треугольникам можно применить теорему Пифагора.
По определению квадрата, все его стороны равны, следовательно катеты этих треугольников равны:
d2=(9√2)2+(9√2)2
d2=2(9√2)2
По первому правилу действий со степенями:
d2=2*92(√2)2
d2=2*81*2=324
d=√324=18
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
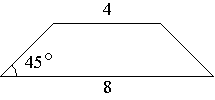 В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Какие из данных утверждений верны? Запишите их номера.
1) Площадь квадрата равна произведению его диагоналей.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Вокруг любого параллелограмма можно описать окружность.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
Комментарии: