
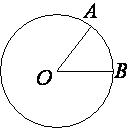
 На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
∠AOB - является
центральным и равен градусной мере дуги, на которую опирается.
Следовательно, градусная мера меньшей дуги AB тоже составляет 40°.
Значит градусная мера большей дуги равна 360°-40°=320°
Пусть х - длина большей дуги, тогда получаем пропорцию:
40° - длина 50
320° - длина х
40/320=50/x
x=320*50/40=8*50=400
Ответ: 400
Поделитесь решением
Присоединяйтесь к нам...
 Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
 Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
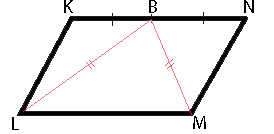 В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
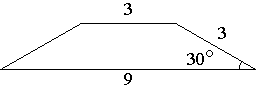 Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
 Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол STV. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол STV. Ответ дайте в градусах.
Комментарии: