
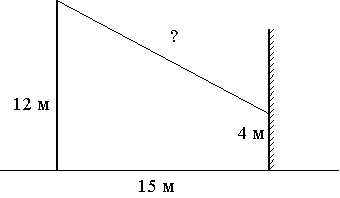
 От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода.
От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода.
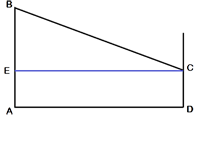 Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD. AECD -
прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD.
Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD. AECD -
прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD.
По
теореме Пифагора BC2=CE2+EB2
BC2=152+(12-4)2
BC2=225+64
BC2=289
BC=√
Ответ: 17
Поделитесь решением
Присоединяйтесь к нам...
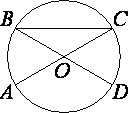 В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
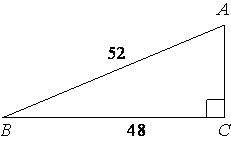 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 Площадь равнобедренного треугольника равна 196√
Площадь равнобедренного треугольника равна 196√
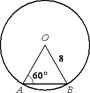 Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
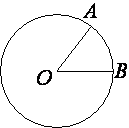 На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
Комментарии:
(2020-03-23 23:38:15) Миннур: Задачи о пересечении биссектрис параллелограмма
(2017-05-14 20:38:10) Администратор: Антон, я добавил уточнение в решение, думаю, так понятно.
(2017-05-14 17:38:41) антон: от куда взяли 17 метров