
 Площадь равнобедренного треугольника равна 196√
Площадь равнобедренного треугольника равна 196√
 Обозначим ключевые точки как показано на рисунке и проведем
высоту BD.
Обозначим ключевые точки как показано на рисунке и проведем
высоту BD.
Высота BD так же является и
медианой, и
биссектрисой (по
третьему свойству равнобедренного треугольника).
Площадь треугольника ABC SABC=(1/2)AC*BD
Так как BD -
медиана, то AC=2AD
Тогда:
SABC=(1/2)2AD*BD=AD*BD
Так как BD еще и
биссектриса, то ∠ABD=∠ABC/2=60°
AD=AB*sin(∠ABD)=AB*sin60°
BD=AB*cos(∠ABD)=AB*cos60°
Тогда:
SABC=AB*sin60°*AB*cos60°=AB2(√
AB2/4=196
AB2=784
AB=28
Ответ: 28
Поделитесь решением
Присоединяйтесь к нам...
 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
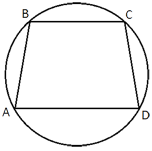 Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
 Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 9 м. Найдите длину троса.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 9 м. Найдите длину троса.
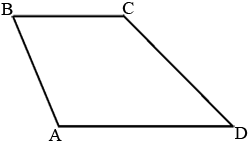 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
Комментарии: