В трапеции ABCD AB=CD, ∠BDA=54° и ∠BDC=33°. Найдите угол ABD. Ответ дайте в градусах.
∠ADC=∠BDA+∠BDC=54°+33°=87°.
Трапеция ABCD -
равнобедренная (т.к. AB=CD), следовательно, по
свойству равнобедренной трапеции, ∠BAD=∠ADC=87°.
Сумма углов любого выпуклого n-угольника равна 180°*(n-2).
Тогда сумма углов трапеции равна 180°*(4-2)=360°, следовательно ∠ABC+∠BCD=360°-87°-87°=186°
По тому же
свойству равнобедренной трапеции ∠ABC=∠BCD, тогда каждый из этих углов равен 186°/2=93°
В любой трапеции основания параллельны (по
определению), т.е. AD||BC, тогда, рассматривая BD как секущую, заметим, что ∠CBD=∠BDA=54° (т.к. это
внутренние накрест лежащие углы).
Тогда ∠ABD=∠ABC-∠CBD=93°-54°=39°
Ответ: 39
Поделитесь решением
Присоединяйтесь к нам...
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
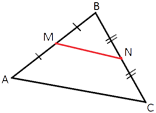Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=24. Найдите MN.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и BDA подобны.
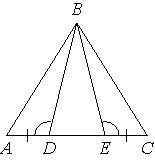На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-10-04 18:10:11) Администратор: Без вопроса, нет ответа.
(2017-10-03 15:43:18) : в трапеции авсд известно что ав сд угол вда 30 и угол вдс 110