Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
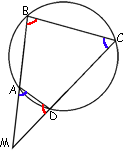Чтобы четырехугольник можно было вписать в окружность, должно выполняться условие:
∠DAB+∠BCD=∠ABC+∠CDA=180° (по третьему свойству описанной окружности
).
∠ADM является
смежным по отношению к ∠CDA, следовательно:
180°=∠ADM+∠CDA
180°=∠ABC+∠CDA (это мы установили ранее).
Получается, что ∠ADM=∠ABC
∠DAM является
смежным по отношению к ∠DAB, следовательно:
180°=∠DAM+∠DAB
180°=∠BCD+∠DAB (это мы установили ранее).
Получается, что ∠DAM=∠BCD
∠M - общий для треугольников MBC и MDA.
Тогда, по
первому признаку подобия, данные треугольники
подобны.
Поделитесь решением
Присоединяйтесь к нам...
Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
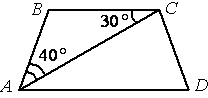Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
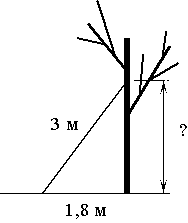Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-05-19 13:34:45) Администратор: Spektra542, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2019-05-14 13:05:07) Spektra542: известно что около четырёхугольника ABCD можно описать окружность и что продолжения сторон пересекаются в точке K. Докажите что углы BAD и KCD равны