
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
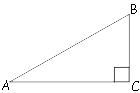 Площадь
прямоугольного треугольника равна половине произведения катетов:
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2
Пусть 30-и градусам равен угол BAC.
Тангенс BAC:
td∠BAC=tg30°=BC/AC=√
AC=BC/(√
S=(BC/(√
BC2=50√
BC=10
sin∠BAC=BC/AB (по
определению).
sin30°=10/AB (sin30°=1/2 по
таблице)
1/2=10/AB
AB=20
Ответ: 20
Поделитесь решением
Присоединяйтесь к нам...
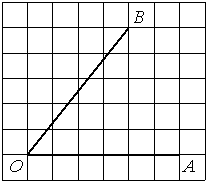 Найдите тангенс угла AOB, изображённого
на рисунке.
Найдите тангенс угла AOB, изображённого
на рисунке.
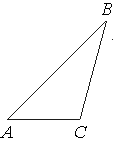 В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
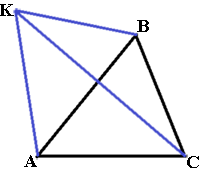 Стороны AC, AB, BC треугольника ABC равны 2√
Стороны AC, AB, BC треугольника ABC равны 2√
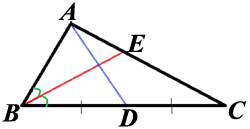 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
Комментарии:
(2016-04-09 23:21:28) Елена: извините увидела
(2016-04-09 23:21:05) Администратор: Елена, AB и есть гипотенуза, ее длина равна 20.
(2016-04-09 23:20:09) Елена: извините,длина гипотенузы
(2016-04-09 23:19:25) Елена: а где гипотенуза