Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
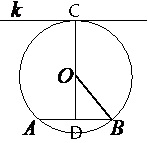Проведем отрезок OB как показано на рисунке.
Расстояние от
хорды AB до параллельной ей
касательной k обозначено как CD.
CD=OC+OD, OC - это радиус окружности, найдем OD.
По условию задачи k||AB. CD перпендикулярен k (по
свойству касательной), тогда CD перпендикулярен и AB (т.к. CD - секущая для параллельных прямых, и внутренние
накрест-лежащие углы равны), значит треугольник OBD
прямоугольный.
DB=AB/2=96/2=48 (по
второму свойству хорды)
OB равен радиусу окружности.
Тогда по
теореме Пифагора:
OB2=OD2+DB2
502=OD2+482
2500=OD2+2304
OD2=2500-2304=196
OD=14
CD=OC+OD=50+14=64
Ответ: 64
Поделитесь решением
Присоединяйтесь к нам...
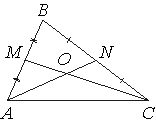Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=18, CM=21. Найдите OM.
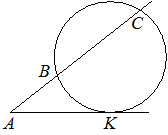Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=8, BC=24. Найдите AK.
Катеты прямоугольного треугольника равны √
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=18, а сторона BC в 1,2 раза меньше стороны AB.
Укажите номера верных утверждений.
1) Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая медиана равнобедренного треугольника является его биссектрисой.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: