
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ25 –Η–Ζ 1087 |
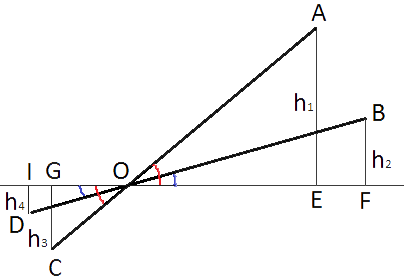
 –ù–Α ―Ä–Η―¹―É–Ϋ–Κ–Β –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ –Κ–Ψ–Μ–Ψ–¥–Β―Ü ―¹ ¬Ϊ–Ε―É―Ä–Α–≤–Μ―ë–Φ¬Μ. –ö–Ψ―Ä–Ψ―²–Κ–Ψ–Β –Ω–Μ–Β―΅–Ψ –Η–Φ–Β–Β―² –¥–Μ–Η–Ϋ―É 2 –Φ, –Α –¥–Μ–Η–Ϋ–Ϋ–Ψ–Β –Ω–Μ–Β―΅–Ψ βÄî 6 –Φ. –ù–Α ―¹–Κ–Ψ–Μ―¨–Κ–Ψ –Φ–Β―²―Ä–Ψ–≤ –Ψ–Ω―É―¹―²–Η―²―¹―è –Κ–Ψ–Ϋ–Β―Ü –¥–Μ–Η–Ϋ–Ϋ–Ψ–≥–Ψ –Ω–Μ–Β―΅–Α, –Κ–Ψ–≥–¥–Α –Κ–Ψ–Ϋ–Β―Ü –Κ–Ψ―Ä–Ψ―²–Κ–Ψ–≥–Ψ –Ω–Ψ–¥–Ϋ–Η–Φ–Β―²―¹―è –Ϋ–Α 0,5 –Φ?
–ù–Α ―Ä–Η―¹―É–Ϋ–Κ–Β –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ –Κ–Ψ–Μ–Ψ–¥–Β―Ü ―¹ ¬Ϊ–Ε―É―Ä–Α–≤–Μ―ë–Φ¬Μ. –ö–Ψ―Ä–Ψ―²–Κ–Ψ–Β –Ω–Μ–Β―΅–Ψ –Η–Φ–Β–Β―² –¥–Μ–Η–Ϋ―É 2 –Φ, –Α –¥–Μ–Η–Ϋ–Ϋ–Ψ–Β –Ω–Μ–Β―΅–Ψ βÄî 6 –Φ. –ù–Α ―¹–Κ–Ψ–Μ―¨–Κ–Ψ –Φ–Β―²―Ä–Ψ–≤ –Ψ–Ω―É―¹―²–Η―²―¹―è –Κ–Ψ–Ϋ–Β―Ü –¥–Μ–Η–Ϋ–Ϋ–Ψ–≥–Ψ –Ω–Μ–Β―΅–Α, –Κ–Ψ–≥–¥–Α –Κ–Ψ–Ϋ–Β―Ü –Κ–Ψ―Ä–Ψ―²–Κ–Ψ–≥–Ψ –Ω–Ψ–¥–Ϋ–Η–Φ–Β―²―¹―è –Ϋ–Α 0,5 –Φ?
 –†–Η―¹―É–Ϋ–Ψ–Κ,–Ω―Ä–Β–¥–Μ–Ψ–Ε–Β–Ϋ–Ϋ―΄–Ι –≤ –Ζ–Α–¥–Α―΅–Β –Φ–Ψ–Ε–Ϋ–Ψ ―É―¹–Μ–Ψ–≤–Ϋ–Ψ –Ω–Β―Ä–Β―Ä–Η―¹–Ψ–≤–Α―²―¨ –≤ –≤–Η–¥–Β ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤.
–†–Η―¹―É–Ϋ–Ψ–Κ,–Ω―Ä–Β–¥–Μ–Ψ–Ε–Β–Ϋ–Ϋ―΄–Ι –≤ –Ζ–Α–¥–Α―΅–Β –Φ–Ψ–Ε–Ϋ–Ψ ―É―¹–Μ–Ψ–≤–Ϋ–Ψ –Ω–Β―Ä–Β―Ä–Η―¹–Ψ–≤–Α―²―¨ –≤ –≤–Η–¥–Β ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤.
h1 - –Η–Ζ–Ϋ–Α―΅–Α–Μ―¨–Ϋ–Α―è –≤―΄―¹–Ψ―²–Α –¥–Μ–Η–Ϋ–Ϋ–Ψ–≥–Ψ –Ω–Μ–Β―΅–Α –Ε―É―Ä–Α–≤–Μ―è.
h2 - –Κ–Ψ–Ϋ–Β―΅–Ϋ–Α―è –≤―΄―¹–Ψ―²–Α –¥–Μ–Η–Ϋ–Ϋ–Ψ–≥–Ψ –Ω–Μ–Β―΅–Α –Ε―É―Ä–Α–≤–Μ―è.
h3 - –Η–Ζ–Ϋ–Α―΅–Α–Μ―¨–Ϋ–Α―è –≤―΄―¹–Ψ―²–Α –Κ–Ψ―Ä–Ψ―²–Κ–Ψ–≥–Ψ –Ω–Μ–Β―΅–Α –Ε―É―Ä–Α–≤–Μ―è.
h4 - –Κ–Ψ–Ϋ–Β―΅–Ϋ–Α―è –≤―΄―¹–Ψ―²–Α –Κ–Ψ―Ä–Ψ―²–Κ–Ψ–≥–Ψ –Ω–Μ–Β―΅–Α –Ε―É―Ä–Α–≤–Μ―è.
h3-h4=0,5 –Φ–Β―²―Ä–Α (–Ω–Ψ ―É―¹–Μ–Ψ–≤–Η―é –Ζ–Α–¥–Α―΅–Η).
–ù–Α–Φ –Ϋ–Α–¥–Ψ –Ϋ–Α–Ι―²–Η:
h1-h2=?.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η AOE –Η COG.
1) ∠AOE=∠COG, ―².–Κ. –Ψ–Ϋ–Η
–≤–Β―Ä―²–Η–Κ–Α–Μ―¨–Ϋ―΄–Β.
2) ∠AEO=∠CGO=90¬Α
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η AOE –Η COG
–Ω–Ψ–¥–Ψ–±–Ϋ―΄ (–Ω–Ψ –Ω–Β―Ä–≤–Ψ–Φ―É –Ω―Ä–Η–Ζ–Ϋ–Α–Κ―É –Ω–Ψ–¥–Ψ–±–Η―è). –û―²―¹―é–¥–Α ―¹–Μ–Β–¥―É–Β―², ―΅―²–Ψ h1/OA=h3/OC.
–Δ―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η BOF –Η DOI ―²–Ψ–Ε–Β
–Ω–Ψ–¥–Ψ–±–Ϋ―΄ (–Α–Ϋ–Α–Μ–Ψ–≥–Η―΅–Ϋ–Ψ –Ω―Ä–Β–¥―΄–¥―É―â–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α–Φ).
–Δ–Ψ–≥–¥–Α:
h2/OB=h4/OD
OA=OB –Η OC=OD (―²–Α–Κ –Κ–Α–Κ –¥–Μ–Η–Ϋ―΄ –Ω–Μ–Β―΅ –Ε―É―Ä–Α–≤–Μ―è –Ϋ–Β –Φ–Β–Ϋ―è―é―²―¹―è), ―²–Ψ–≥–¥–Α:
h2/OA=h4/OC
–£―΄―΅―²–Β–Φ –Η–Ζ –Ω–Β―Ä–≤–Ψ–≥–Ψ ―Ä–Α–≤–Β–Ϋ―¹―²–≤–Α –≤―²–Ψ―Ä–Ψ–Β:
h1/OA-h2/OA=h3/OC-h4/OC.
(h1-h2)/OA=(h3-h4)/OC.
(h1-h2)/6=0,5/2.
h1-h2=6*0,5/2=1,5.
–û―²–≤–Β―²: 1,5.
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ –êD–Γ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD, –Β―¹–Μ–Η –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ –ê–Γ –Ψ–±―Ä–Α–Ζ―É–Β―² ―¹ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β–Φ –£–Γ –Η –±–Ψ–Κ–Ψ–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι –ê–£ ―É–≥–Μ―΄, ―Ä–Α–≤–Ϋ―΄–Β
30¬Α –Η 50¬Α ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ.
–ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ –êD–Γ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD, –Β―¹–Μ–Η –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ –ê–Γ –Ψ–±―Ä–Α–Ζ―É–Β―² ―¹ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β–Φ –£–Γ –Η –±–Ψ–Κ–Ψ–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι –ê–£ ―É–≥–Μ―΄, ―Ä–Α–≤–Ϋ―΄–Β
30¬Α –Η 50¬Α ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ.
 –Δ–Ψ―΅–Κ–Α –û βÄ™ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, /BOC=110¬Α (―¹–Φ. ―Ä–Η―¹―É–Ϋ–Ψ–Κ). –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α BAC (–≤ –≥―Ä–Α–¥―É―¹–Α―Ö).
–Δ–Ψ―΅–Κ–Α –û βÄ™ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, /BOC=110¬Α (―¹–Φ. ―Ä–Η―¹―É–Ϋ–Ψ–Κ). –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α BAC (–≤ –≥―Ä–Α–¥―É―¹–Α―Ö).
 –‰–Ζ ―²–Ψ―΅–Κ–Η –ê –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–≤–Β –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Β –Κ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β –û. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η –ê –¥–Ψ ―²–Ψ―΅–Κ–Η –û, –Β―¹–Μ–Η ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Φ–Η ―Ä–Α–≤–Β–Ϋ 60¬Α, –Α ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 8.
–‰–Ζ ―²–Ψ―΅–Κ–Η –ê –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–≤–Β –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Β –Κ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β –û. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η –ê –¥–Ψ ―²–Ψ―΅–Κ–Η –û, –Β―¹–Μ–Η ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Φ–Η ―Ä–Α–≤–Β–Ϋ 60¬Α, –Α ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 8.
 –‰–Ζ –≤–Β―Ä―à–Η–Ϋ―΄ –Ω―Ä―è–Φ–Ψ–≥–Ψ ―É–≥–Μ–Α C ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Α –≤―΄―¹–Ψ―²–Α CP. –†–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ACP, ―Ä–Α–≤–Β–Ϋ 12 ―¹–Φ, ―²–Α–Ϋ–≥–Β–Ϋ―¹ ―É–≥–Μ–Α ABC ―Ä–Α–≤–Β–Ϋ 2,4. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
–‰–Ζ –≤–Β―Ä―à–Η–Ϋ―΄ –Ω―Ä―è–Φ–Ψ–≥–Ψ ―É–≥–Μ–Α C ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Α –≤―΄―¹–Ψ―²–Α CP. –†–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ACP, ―Ä–Α–≤–Β–Ϋ 12 ―¹–Φ, ―²–Α–Ϋ–≥–Β–Ϋ―¹ ―É–≥–Μ–Α ABC ―Ä–Α–≤–Β–Ϋ 2,4. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
 –ë–Ψ–Κ–Ψ–≤–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Α ―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ–Α 4, –Α –Ψ–¥–Η–Ϋ –Η–Ζ –Ω―Ä–Η–Μ–Β–≥–Α―é―â–Η―Ö –Κ –Ϋ–Β–Ι ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Β–Ϋ
30¬Α. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –Β―¹–Μ–Η –Β―ë –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―Ä–Α–≤–Ϋ―΄ 2 –Η 5.
–ë–Ψ–Κ–Ψ–≤–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Α ―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ–Α 4, –Α –Ψ–¥–Η–Ϋ –Η–Ζ –Ω―Ä–Η–Μ–Β–≥–Α―é―â–Η―Ö –Κ –Ϋ–Β–Ι ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Β–Ϋ
30¬Α. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –Β―¹–Μ–Η –Β―ë –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―Ä–Α–≤–Ϋ―΄ 2 –Η 5.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2015-05-21 21:34:00) –ï–Μ–Β–Ϋ–Α: –û–Ω―É―¹–Κ–Α–Β–Φ –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä―΄ –Η–Ζ –Γ –Ϋ–Α –£D –Η –Η–Ζ –ê –Ϋ–Α –£D. –ü–Ψ–Μ―É―΅–Β–Ϋ–Ϋ―΄–Β ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η –Ω–Ψ–¥–Ψ–±–Ϋ―΄, ―².–Κ. –Ω―Ä–Ψ–≤–Β–¥―ë–Ϋ–Ϋ―΄–Β –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä―΄ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄ –¥―Ä―É–≥ –¥―Ä―É–≥―É. –î–Α–Μ―¨―à–Β ―¹–Ψ―¹―²–Α–≤–Μ―è–Β–Φ –Ω―Ä–Ψ–Ω–Ψ―Ä―Ü–Η―é –Η –Ϋ–Α―Ö–Ψ–¥–Η–Φ –Ϋ–Β–Η–Ζ–≤–Β―¹―²–Ϋ―΄–Ι –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä.
(2015-03-14 13:23:46) –ù–Η–Κ–Ψ–Μ–Α–Ι: –ê –Β―â―ë –Φ–Ψ–Ε–Ϋ–Ψ –Ϋ–Α –≥–Μ–Α–Ζ –Ψ–Ω―Ä–Β–¥–Β–Μ–Η―²―¨, –Ω–Ψ –Κ–Μ–Β―²–Ψ―΅–Κ–Α–Φ))