
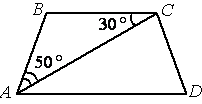 Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
В треугольнике ABC угол /ABC=180°-/BAC-/BCA=180°-50°-30°=100° (по
теореме о сумме углов треугольника).
Любую
равнобедренную трапецию можно вписать в окружность (
свойство описанной окружности), следовательно, сумма противоположных углов трапеции равна 180° по
третьему свойству описанной окружности. Следовательно, /ABC+/ADC=180°
/ADC=180°-100°=80°.
Ответ: /ADC=80°.
Поделитесь решением
Присоединяйтесь к нам...
 Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=7 и HD=24. Диагональ параллелограмма BD равна 51. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=7 и HD=24. Диагональ параллелограмма BD равна 51. Найдите площадь параллелограмма.
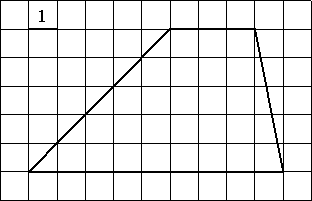 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
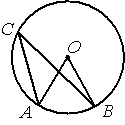 Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
Комментарии: