
 Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
Радиус вписанной окружности можно вычислить по формуле R=(AC+CB-AB)/2. Для этого необходимо вычислить длины всех сторон данного треугольника.
Рассмотрим треугольник ABC.
По
определению tgABC=AC/CB=2,4 => CB=AC/2,4.
По
теореме Пифагора AB2=AC2+CB2
AB2=AC2+(AC/2,4)2
AB2=6,76*AC2/5,76
AB=2,6*AC/2,4=1,3*AC/1,2
Необходимо вычислить AC.
По
теореме о сумме углов треугольника для треугольника ABC:
/CAB=180°-90°-/ABC
Для треугольника ACP:
/CAB=180°-90°-/ACP
Следовательно, /ABC=/ACP.
Рассмотрим треугольник ACP.
По
определению tgACP=AP/CP=2,4 => AP=2,4*CP.
По
теореме Пифагора AC2=CP2+AP2
AC2=CP2+(2,4*CP)2
AC2=6,76*CP2
AC=2,6*CP
CP=AC/2,6
r=(AP+CP-AC)/2
2*r=2,4*CP+CP-AC
2*r=3,4CP-AC
2*12=3,4*AC/2,6-AC
24=0,8*AC/2,6
30=AC/2,6
78=AC
Вычислив AC, мы можем вычислить AB и CP, указанные выше:
AB=1,3*AC/1,2=1,3*78/1,2=13*78/12=13*26/4=84,5
CB=AC/2,4=78/2,4=32,5
R=(AC+CB-AB)/2, тогда получаем:
R=(78+32,5-84,5)/2=13.
Ответ: R=13.
Поделитесь решением
Присоединяйтесь к нам...
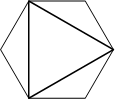 Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
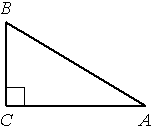 В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
 Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 62°, 54° и 64°.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 62°, 54° и 64°.
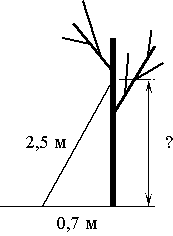 Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
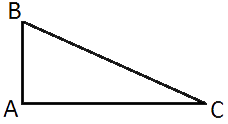 В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
Комментарии: