
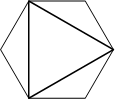
 Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
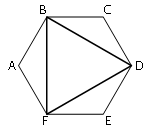 Рассмотрим треугольники FAB, BCD и DEF.
Рассмотрим треугольники FAB, BCD и DEF.
Т.к. шестиугольник
правильный, то FA=AB=BC=CD=DE=EF и углы /FAB=/BCD=/DEF. Значит рассматриваемые треугольники равны (по
первому признаку равенства). Следовательно, FB=BD=DF. Т.е. треугольник BDF -
равносторонний.
Поделитесь решением
Присоединяйтесь к нам...
 Катет и гипотенуза прямоугольного треугольника равны 15 и 39. Найдите высоту, проведенную к гипотенузе.
Катет и гипотенуза прямоугольного треугольника равны 15 и 39. Найдите высоту, проведенную к гипотенузе.
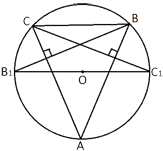 Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
 Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=6, AD=13, AC=38. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=6, AD=13, AC=38. Найдите AO.
 Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
Комментарии: