Сторона ромба равна 36, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
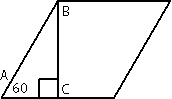Рассмотрим треугольник АВС.
Этот треугольник
прямоугольный (по условию задачи).
∠С=90°, так как это прямой угол.
∠A=60°, следовательно по
теореме о сумме углов треугольника:
180° = ∠АВС + ∠А + ∠С
180° = ∠АВС + 60° + 90°
∠АВС = 180°-90°-60°=30°.
По
свойству прямоугольного треугольника:
АС=АВ/2=36/2=18.
Следовательно вторая половина стороны ромба = 36-18=18.
Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: 18 и 18.
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
В трапеции ABCD AB=CD, ∠BDA=67° и ∠BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 169°, угол ABC равен 160°. Найдите угол ACB. Ответ дайте в градусах.
Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению двух его смежных сторон.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-11-26 20:34:53) Администратор: марк, я внес уточнения в решение задачи, так понятней?
(2016-11-25 20:25:34) марк : откуда взялось 90 ° ?
(2015-04-19 11:27:53) Администратор: Алина, АВ - это сторона ромба, а по условию она равна 36.
(2015-04-19 09:54:27) Алина: Почему АВ стало равным 36?