
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
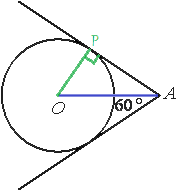 Проведем отрезок АО, данный отрезок равен 6 (по условию задачи).
Проведем отрезок АО, данный отрезок равен 6 (по условию задачи).
Обозначим одну из точек касания окружности и касательной как Р.
Проведем отрезок ОР.
ОР является перпендикуляром к касательной АР (по свойству касательной).
Рассмотрим треугольник АОР. Данный треугольник является прямоугольным,т.к. ОР перпендикулярен АР.
АО является биссектрисой угла, образованного касательными (свойство касательных прямых).
Соответственно угол РАО равен половине данного угла, т.е. 30°.
sin∠PAO=sin30°=1/2 (табличное значение)
sin∠PAO=ОР/АО (по определению синуса).
Получаем:
1/2=ОР/АО
OP=AO/2=6/2=3
Это и есть радиус окружности.
Ответ: 3
Поделитесь решением
Присоединяйтесь к нам...
 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
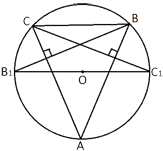 Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
 В прямоугольном треугольнике катет и гипотенуза равны 7 и 25 соответственно. Найдите другой катет этого треугольника.
В прямоугольном треугольнике катет и гипотенуза равны 7 и 25 соответственно. Найдите другой катет этого треугольника.
 Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Комментарии:
(2020-03-09 21:23:59) Администратор: Анастасия, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2020-03-02 21:25:57) Анастасия: Найдите боковую сторону AB трапеции ABCD , если угол ABC и BCD соответственно равны 45 градусов и 150 градусов ,а CD равен 32.
(2016-12-10 20:43:08) Администратор: Дина, да, можно, если сослаться на соответствующую теорему. А лично я против заучивания, зубрежки лишних теорем, я за понимание. На самом деле можно не запоминать и половину материала, который дается в школе, нужно понять основы. Тогда все остальное выстраивается само и большинство свойств, признаков и теорем - это выводы вытекающие из основ. Поэтому я применил именно синус угла, а не теорему, которая вытекает из него.
(2016-12-10 16:56:31) Дина: можно было объяснить проще в данном случае, что катет в прямоугольном треугольнике напротив 30 градусов равен половине гипотенузы
(2016-05-22 16:08:26) Анжела: Благодарю) прекрасное решение))
(2015-12-06 12:44:40) Светлана: Просто замечательно, СПАСИБО огромное!!!
(2015-05-26 14:36:13) Анна: Нормалек :) спасибо большое!)
(2015-05-09 14:24:59) Администратор: Акакий, спасибо, исправлено!
(2015-05-06 19:34:55) Акакий: У вас в определение синуса вместо слова "катета" написано слово "катеРа". Сайт очень хороший,помогает мне к подготовке.Спасибо за то ,что вы есть.
(2015-04-02 23:54:52) Администратор: Света, совершенно верно, упомянутая Вами теорема, как раз, доказывается через синус.
(2015-04-02 23:50:55) Света: можно найти катете проще: катет,лежащий напротив угла=30 градусов равен половине гипотенузы
(2015-03-25 15:01:49) Администратор: Если будет 80 градусов, а не 60, то нужно будет вычислять sin40 - а это уже не 1/2.
(2015-03-25 15:00:11) Администратор: sin30=OP/OA=1/2 - это табличное значение, следовательно OP=OA/2.
(2015-03-24 14:02:56) : а почему ОР равняется половине АО?
(2015-03-24 11:52:37) Дима: А если например будет 80 градус то =40=4 ?
(2015-03-22 15:32:38) Администратор: Катя, уточните, пожалуйста, с какого момента Вы не понимаете?
(2015-03-22 14:51:11) Катя: спасибо)хороший сайт))но я не поимаю ((
(2015-02-28 23:09:09) Администратор: Костя, все правильно написано. Отрезок АО равен 6, 60 - это 60 градусов.
(2015-02-28 20:18:56) Администратор: Костя, все правильно написано. Отрезок АО равен 6, 60 - это 60 градусов.
(2015-02-28 18:36:42) костя: Проведем отрезок АО, данный отрезок равен 6 (по условию задачи). вы не правильно написали не 6 а 60