
Стороны AC, AB, BC треугольника ABC равны 2√
 По условию задачи /KAC>90°, т.е. это наибольший угол в треугольнике AKC следовательно, сторона KC, противолежащая этому углу тоже наибольшая (по теореме о соотношениях между сторонами и углами треугольника). Сторона AC равная 2√
По условию задачи /KAC>90°, т.е. это наибольший угол в треугольнике AKC следовательно, сторона KC, противолежащая этому углу тоже наибольшая (по теореме о соотношениях между сторонами и углами треугольника). Сторона AC равная 2√
По условию задачи треугольник KAC подобен исходному треугольнику ABC. А значит углы этих треугольников соответственно равны (по определению подобных треугольников). Поэтому наибольшие углы двух рассматриваемых треугольников равны, т.е. /KAC=/ABC. /ACK не равен /ACB ( т.к. KC пересекает сторону AB в точке, отличной от B), поэтому /ACK = /BAC. Следовательно, /AKC=/ACB => cos(/AKC)=cos(/ACB).
Применяя теорему косинусов мы можем записать AB2=AC2+BC2-2*AC*BC*cos(/ACB).
(√
13=4*5+4-8*√
13-24=-8*√
11=8*√
cos(/AKC)=cos(/ACB)=11/(8*√
Ответ: cos(/AKC)=11/(8*√
Поделитесь решением
Присоединяйтесь к нам...
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=12 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=12 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
 Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
 Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
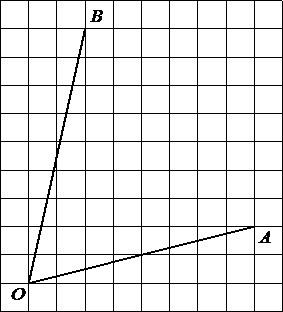 Найдите тангенс угла
AOB.
Найдите тангенс угла
AOB.
 Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Комментарии:
(2015-12-24 10:59:42) Егор: Очень хорошая задача!