
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
 Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Рассмотрим треугольники ABC и DCE, эти треугольники
подобны, т.к. /C - общий, /B и /DEC - прямые, а углы A и EDC - равны, так как являются
соответственними.
Из подобия этих треугольников следует, что AB/DE=BC/EC, отсюда BC=(AB*EC)/DE=(9*1)/2=4,5.
В задаче нас интересует отрезок BE, BE=BC-EC=4,5-1=3,5.
Ответ: от фонаря человек стоит на расстоянии 3,5 м.
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C равен 90°, sinA=0,75, AC=√
В треугольнике ABC угол C равен 90°, sinA=0,75, AC=√
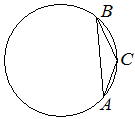 В треугольнике ABC угол C равен 135°, AB=14√2. Найдите радиус окружности, описанной около этого треугольника.
В треугольнике ABC угол C равен 135°, AB=14√2. Найдите радиус окружности, описанной около этого треугольника.
 В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Комментарии:
(2015-04-01 22:42:05) Администратор: BC=(AB*EC)/DE=(9*1)/2=4,5 Не понимаю сути вопроса.
(2015-04-01 16:30:03) : почему вс = 4,5?