
 Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
Обозначим ширину окантовки как х.
Тогда ширина бумаги будет (2х+24) см (2х потому, что окантовка с обоих сторон от картинки).
Высока бумаги - (2х+37) см.
Sбумаги=(2х+37)(2х+24)=1440
4x2+48x+74x+888=1440
4x2+122x+888=1440
4x2+122x-552=0
x2+30,5x-138=0
Решим это
квадратное уравнение:
D=30,52-4*1*(-138)=930,25+552=1482,25
x1=(-30,5+38,5)/2=4
x2=(-30,5-38,5)/2=-34,5
Отрицательный ответ нам не подходит, следовательно, ширина окантовки 4 см.
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
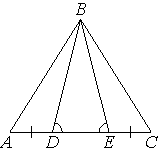 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
 Радиус окружности, описанной около квадрата, равен 14√
Радиус окружности, описанной около квадрата, равен 14√
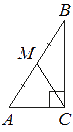 В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.
В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.
Косинус острого угла A треугольника ABC равен 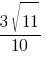 . Найдите sinA.
. Найдите sinA.
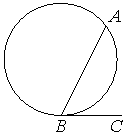 На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Комментарии: