На координатной прямой отмечено число a.
Расположите в порядке убывания числа a-1, 1/a, a.
1) a-1, 1/a, a
2) 1/a, a, a-1
3) 1/a, a-1, a
4) a, 1/a, a-1
Отметим, что число "а" положительное и немного больше 1
Значит a-1>1-1
Значит a-1>0
Заметим, что a-1 немного больше 0, ровно на столько, на сколько а>1.
Теперь разберемся с числом 1/а.
Тут тонкий момент:
чем "а" "ближе" к 1, тем 1/a тоже ближе к 1.
Например:
если a=1,1 => 1/a≅0,9
если a=1,8 => 1/a≅0,56
Как уже отмечалось: а немного больше 1, следовательно 1/а будет немного меньше 1.
Значит числа расположатся так: a, 1/a, a-1.
Ответ: 4)
Поделитесь решением
Присоединяйтесь к нам...
Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 4 км/ч, а собственная скорость лодки 6 км/ч?
Найдите корни уравнения x2+3x=18.
Какое из приведённых ниже неравенств является верным при любых значениях a и b, удовлетворяющих условию a<b?
1) a-b>5
2) b-a>3
3) a-b<3
4) b-a<1
Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
На каком рисунке изображено множество решений неравенства x2-4x+3≥0?
1) 
2) 
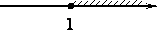
3) 
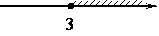
4) 
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: