
Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 4 км/ч, а собственная скорость лодки 6 км/ч?
Обозначим:
S - расстояние от пристани до места рыбалки.
t1 - время движения лодки против течения.
t2 - время движения лодки по течению.
Скорость лодки против течения равна 6-4=2 км/ч, по течению - 6+4=10 км/ч.
Составим уравнения:
движение лодки против течения:
S=2t1
движение лодки по течению:
S=10t2
общее время поездки:
5=t1+t2+2
t1=3-t2
 S=2(3-t2)
S=2(3-t2)
S=10t2
Вычтем из первого уравнения второе:
S-S=2(3-t2)-10t2
0=6-2t2-10t2
0=6-12t2
t2=6/12=0,5 часа
Подставляем во второе уравнение:
S=10t2=10*0,5=5 км.
Ответ: 5
Поделитесь решением
Присоединяйтесь к нам...
На координатной прямой отмечено число c. Расположите в порядке возрастания числа 1c; c; c2.
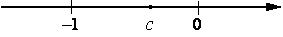
1) c2; c; 1/c
2) c2; 1/c; c
3) 1/c; c; c2
4) 1/c; c2; c
В начале года число абонентов телефонной компании «Запад» составляло 800 тыс. человек, а в конце года их стало 920 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
Решите уравнение x(x2+2x+1)=6(x+1).
В начале года число абонентов телефонной компании «Запад» составляло 800 тыс. человек, а в конце года их стало 920 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
Решите систему уравнений 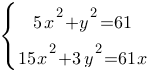
Комментарии: