
Постройте график функции 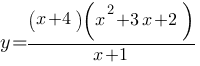 и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Запишем Область Допустимых Значений (ОДЗ).
Так как на ноль делить нельзя, то x+1≠0, т.е. x≠-1
Упростим функцию, для этого разложим x2+3x+2 на множители. Для этого найдем корни уравнения:
x2+3x+2=0
D=32-4*1*2=9-8=1
x1=(-3+1)/(2*1)=-2/2=-1
x2=(-3-1)/(2*1)=-4/2=-2
Тогда, x2+3x+2=(x-(-1))(x-(-2))
x2+3x+2=(x+1)(x+2)
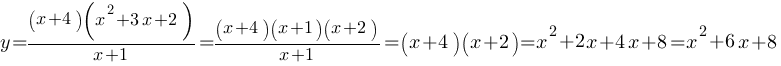
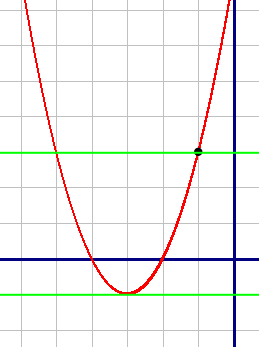 График представляет из себя параболу. Коэффициент а=1, т.е. больше нуля, следовательно ветви параболы направлены вверх. Построим график по точкам:
График представляет из себя параболу. Коэффициент а=1, т.е. больше нуля, следовательно ветви параболы направлены вверх. Построим график по точкам:
| X | -1 | -2 | -3 | -4 |
| Y | 3 | 0 | -1 | 0 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
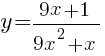
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
A) 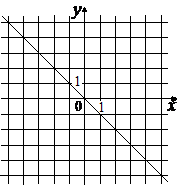 Б)
Б)  В)
В) 
ФОРМУЛЫ
1) y=-x2
2) y=-x
3) y=-1/x
В таблице под каждой буквой укажите соответствующий номер.
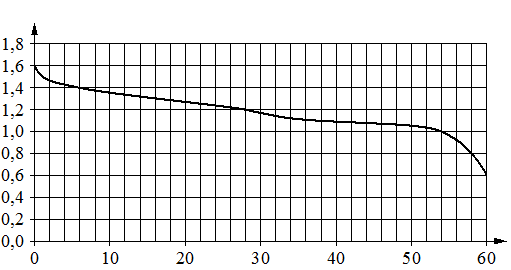 При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,4 В до 0,8 В.
При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,4 В до 0,8 В.
Установите соответствие между функциями и их графиками.
| ФУНКЦИИ | ГРАФИКИ | |
| А) y=(1/3)x+2 Б) y=-4x2+20x-22 В) y=1/x |
1) 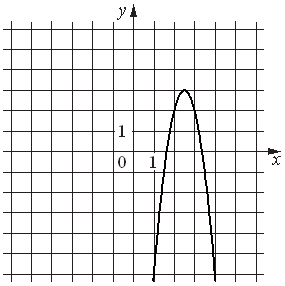 |
2) 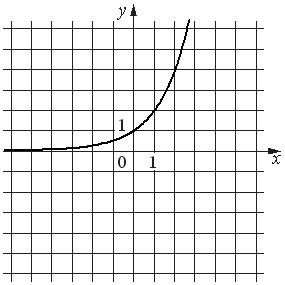 |
3) 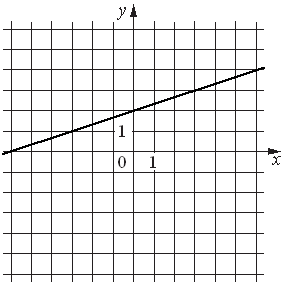 |
4) 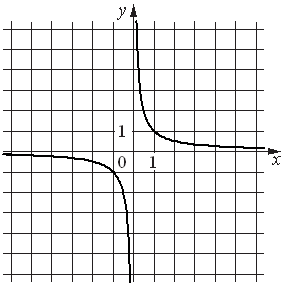 |
Постройте график функции
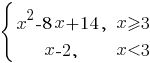
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Комментарии:
(2015-04-22 17:33:58) Администратор: Фразу "было бы правильно , если бы я написал :" при у< 0?" я не понял, перефразируйте, пожалуйста.
(2015-04-22 17:31:00) Администратор: При m1=3 прямая пересекает график в точке (-5;3) и НЕ пересекает в точке (-1;3), так как это выколотая точка, т.е. ее нет в графике. А нам и надо прямую, которая имеет только одну общую точку.
(2015-04-22 17:27:31) Администратор: В упрощенную функцию y=x2+6x+8 подставили x=-1, получили y=(-1)2-6+8=3.
(2015-04-22 17:03:35) : было бы правильно , если бы я написал :" при у< 0?
(2015-04-22 17:01:52) : m1=3. почему так? там же две точки? при х= -5? нет разве?
(2015-04-22 16:59:32) : как вы узнали , что y≠3