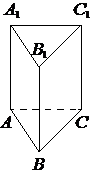
Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.
Объем призмы вычисляется перемножением площади основания призмы на высоту.
Найдем площадь основания.
По
определению правильной призмы, в основании лежит правильный (т.е.
равносторонний) треугольник.
По
пятому свойству равностороннего треугольника:
S=a2√3/4=22√3/4=4√3/4=√3
Зная площадь основания и высоту, вычисляем объем призмы:
V=S*h=√3*4√3=4(√3)2=4*3=12
Ответ: 12
Поделитесь решением
Присоединяйтесь к нам...
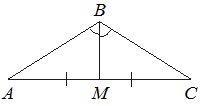В треугольнике ABC угол B равен 120°. Медиана BM делит угол B пополам и равна 27. Найдите длину стороны AB.
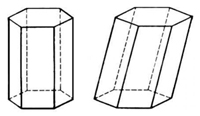
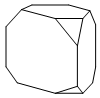От деревянной правильной треугольной призмы отпилили все её вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
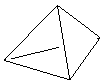Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
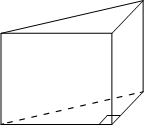В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3,
а гипотенуза равна √
Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: