Задача №20 из 42 |
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
А)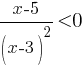 
|
1) 
|
Б)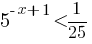 
|
2) 
|
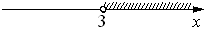
| В) (x-3)(x-5)>0 |
3) 
|
| Г) log2(x-3)<1 |
4) 
|
Решим каждое неравенство:
А)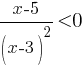
Это неравенство будет меньше нуля, только когда числитель будет меньше нуля, так как знаменатель всегда положителен. Следовательно, данное неравенство можно упростить:
x-5<0 => x<5, подходит вариант 4).
Б)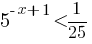
5-x+1<5-2
Применим теорему для решения показательных неравенств:
-x+1<-2 (знак сохраняется так как 5>1)
-x<-3 |*(-1)
x>3 (знак поменялся так как мы домножили на отрицательное число).
Подходит вариант 2).
В) (x-3)(x-5)>0
Найдем корни соответствующего уравнения:
(x-3)(x-5)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) x-3=0 => x1=3
2) x-5=0 => x2=5
x2-5x-3x+15>0
x2-8x+15>0
График данной функции - парабола, коэффициент а=1, т.е. положительный, следовательно ветви параболы направлены вверх.
Функция больше нуля, когда ее график располагается выше оси Х. В данном случае на диапазонах (-∞3) и (5;+∞) - подходит вариант 1).
Г) log2(x-3)<1
По второму свойству логарифмов преобразуем правую часть неравенства:
log2(x-3)
По теореме для решения логарифмических неравенств:
x-3<2
x-3>0
x<5
x>3
Подходит вариант 3).
Ответ:
A)
Б)
В)
Г)
4)
2)
1)
3)
Поделитесь решением
Присоединяйтесь к нам...
Найдите корень уравнения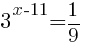 
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) (x-1)2(x-4)<0 | 1) (-∞; 1)∪(4; +∞) |
Б)  |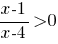
2) (1; 4)∪(4; +∞) |
| В) (x-1)(x-4)<0 | 3) (-∞; 1)∪(1; 4) |
Г)  |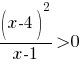
4) (1; 4) |
На координатной прямой отмечено число m и точки A, B, C и D.
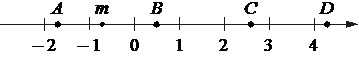
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА |
| A | 1) √ |
| B | 2) m2 |
| C | 3) m-1 |
| D | 4) -3/m |
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) длительность прямого авиаперелёта Москва – Гавана | 1) 14,6 секунды |
| Б) бронзовый норматив ГТО по бегу на 100 м для мальчиков 16–17 лет | 2) 60190 суток |
| В) время одного оборота Нептуна вокруг Солнца | 3) 13 часов |
| Г) длительность эпизода мультипликационного сериала | 4) 22 минуты |
Найдите корень уравнения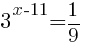
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: