
Парабола проходит через точки A(0; 6), B(6; -6), C(1; 9). Найдите координаты её вершины.
Составим систему уравнений подставив имеющиеся координаты в общую формулу квадратного уравнения:
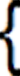 6=a*02+b*0+c
6=a*02+b*0+c
-6=a*62+b*6+c
9=a*12+b*1+c
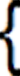 6=c
6=c
-6=a*36+b*6+c
9=a+b+c
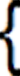 6=c
6=c
-6=36a+6b+6
9=a+b+6
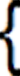 6=c
6=c
-1=6a+b+1
3=a+b
 6=c
6=c
-2=6a+b
3-a=b
 6=c
6=c
-2=6a+(3-a)
3-a=b
 6=c
6=c
-2=6a+3-a
3-a=b
 6=c
6=c
-5=5a
3-a=b
 6=c
6=c
-1=a
3-a=b
 6=c
6=c
-1=a
3-(-1)=b
 6=c
6=c
-1=a
4=b
Значит наше уравнение имеет вид: y=-x2+4x+6
Координаты вершины вычисляются по соответствующим
формулам:
x0=-4/(2(-1))=2
y0=(4*(-1)*6-42)/(4*(-1))=(-24-16)/(-4)=(-40)/(-4)=10
Ответ: (2; 10)
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения 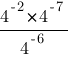
1) -1/64
2) 64
3) 1/64
4) -64
Какое из данных ниже чисел является значением выражения 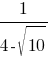 ?
?
1) 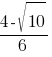
2) 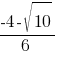
3) 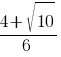
4) 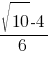
Сократите дробь 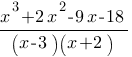
Значение какого из выражений является числом иррациональным?
1) √
2) (√
3) √
4) √
Решите уравнение (x-3)(x-4)(x-5)=(x-2)(x-4)(x-5).
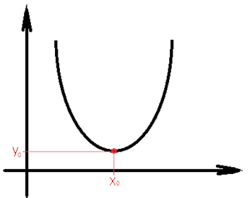 Координаты вершины параболы y=ax2+bx+c можно найти по вормулам:
Координаты вершины параболы y=ax2+bx+c можно найти по вормулам: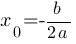
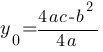
Комментарии:
(2016-05-29 12:24:09) Администратор: Елена, как у Вас получилось -8?
(2016-05-29 11:05:54) Елена: вершина у = -8