
Постройте график функции
y=x|x|-|x|-2x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Данная функция содержит
модуль, следовательно ее нужно разложить на две функции:
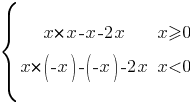
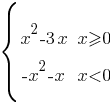
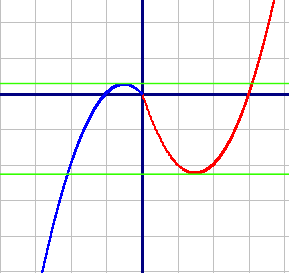 Обе подфункции - параболы. Построим их по точкам:
Обе подфункции - параболы. Построим их по точкам:
y1=x2-3x на диапазоне от 0 до плюс бесконечности (красный график):
| X | 0 | 1 | 2 | 3 | 4 |
| Y | 0 | -2 | -3 | 0 | 4 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 0 | -2 | -6 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции 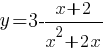
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Постройте график функции
y=|x2-x-2|.
Какое наибольшее число общих точек может иметь график данной функции с прямой, параллельной оси абсцисс?
Постройте график функции 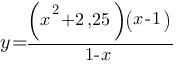 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
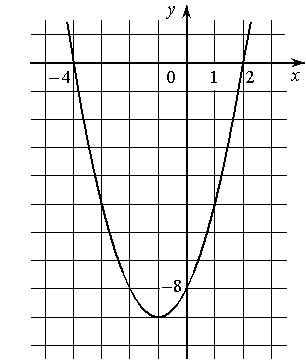 На рисунке изображён график квадратичной функции y=ƒ(x).
На рисунке изображён график квадратичной функции y=ƒ(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) Функция убывает на промежутке [-1;+∞)
2) ƒ(x)>0 при x<-4 и при x>2
3) Наименьшее значение функции равно -9
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=2/5x+2 2) y=2/5x-2 3) y=-2/5x-2 4) y=-2/5x+2 |
А) 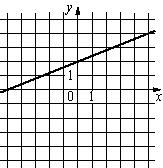 |
Б) 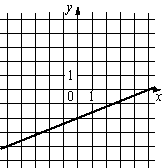 |
В) 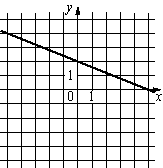 |
Комментарии: