
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ61 –Є–Ј 287 |
–Э–∞ —А–Є—Б—Г–љ–Ї–µ –Є–Ј–Њ–±—А–∞–ґ–µ–љ—Л –≥—А–∞—Д–Є–Ї–Є —Д—Г–љ–Ї—Ж–Є–є –≤–Є–і–∞ y=ax2+bx+c. –£—Б—В–∞–љ–Њ–≤–Є—В–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–µ –Љ–µ–ґ–і—Г –≥—А–∞—Д–Є–Ї–∞–Љ–Є —Д—Г–љ–Ї—Ж–Є–є –Є –Ј–љ–∞–Ї–∞–Љ–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ a –Є c.
| –Ъ–Ю–≠–§–§–Ш–¶–Ш–Х–Э–Ґ–Ђ | –У–†–Р–§–Ш–Ъ–Ш | ||
|
1) a>0, c>0 2) a>0, c<0 3) a<0, c>0 4) a<0, c<0 |
–Р)  |
–С)  |
–Т)  |
–Х—Б–ї–Є —Г –Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В "–∞" –±–Њ–ї—М—И–µ –љ—Г–ї—П, —В–Њ –≤–µ—В–≤–Є –њ–∞—А–∞–±–Њ–ї—Л –љ–∞–њ—А–∞–≤–ї–µ–љ—Л –≤–≤–µ—А—Е.
–Ш –љ–∞–Њ–±–Њ—А–Њ—В, –µ—Б–ї–Є —Г –Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В "–∞" –Љ–µ–љ—М—И–µ –љ—Г–ї—П, —В–Њ –≤–µ—В–≤–Є –њ–∞—А–∞–±–Њ–ї—Л –љ–∞–њ—А–∞–≤–ї–µ–љ—Л –≤–љ–Є–Ј.
–Ч–љ–∞–Ї –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞ "—Б" –Љ–Њ–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М –њ–Њ —В–Њ—З–Ї–µ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –њ–∞—А–∞–±–Њ–ї—Л —Б –Њ—Б—М—О Y. –Х—Б–ї–Є —В–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –≤—Л—И–µ –љ—Г–ї—П, —В–Њ –Є "—Б" –±–Њ–ї—М—И–µ –љ—Г–ї—П. –Ш –љ–∞–Њ–±–Њ—А–Њ—В, –µ—Б–ї–Є —В–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –љ–Є–ґ–µ –љ—Г–ї—П, —В–Њ –Є "—Б" –Љ–µ–љ—М—И–µ –љ—Г–ї—П. –Р –µ—Б–ї–Є –њ–∞—А–∞–±–Њ–ї–∞ –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј –љ–∞—З–∞–ї–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В, —В–Њ —Б=0
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –Ї–∞–ґ–і—Л–є –≥—А–∞—Д–Є–Ї:
–Р) –Т–µ—В–≤–Є –њ–∞—А–∞–±–Њ–ї—Л –љ–∞–њ—А–∞–≤–ї–µ–љ—Л –≤–≤–µ—А—Е. –Ґ–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –њ–∞—А–∞–±–Њ–ї—Л —Б –Њ—Б—М—О Y –ї–µ–ґ–Є—В –≤—Л—И–µ –љ—Г–ї—П, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ a>0 –Є c>0, —В.–µ. –≤–∞—А–Є–∞–љ—В 1).
–С) –Т–µ—В–≤–Є –њ–∞—А–∞–±–Њ–ї—Л –љ–∞–њ—А–∞–≤–ї–µ–љ—Л –≤–љ–Є–Ј. –Ґ–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –њ–∞—А–∞–±–Њ–ї—Л —Б –Њ—Б—М—О Y –ї–µ–ґ–Є—В –≤—Л—И–µ –љ—Г–ї—П, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ a<0, –∞ c>0, —В.–µ. –≤–∞—А–Є–∞–љ—В 3).
–Т) –Т–µ—В–≤–Є –њ–∞—А–∞–±–Њ–ї—Л –љ–∞–њ—А–∞–≤–ї–µ–љ—Л –≤–≤–µ—А—Е. –Ґ–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –њ–∞—А–∞–±–Њ–ї—Л —Б –Њ—Б—М—О Y –ї–µ–ґ–Є—В –љ–Є–ґ–µ –љ—Г–ї—П, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ a>0, –∞ c<0, —В.–µ. –≤–∞—А–Є–∞–љ—В 2).
–Ю—В–≤–µ—В: –Р) - 1), –С) - 3), –Т) - 2)
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
–Э–∞ —А–Є—Б—Г–љ–Ї–∞—Е –Є–Ј–Њ–±—А–∞–ґ–µ–љ—Л –≥—А–∞—Д–Є–Ї–Є —Д—Г–љ–Ї—Ж–Є–є –≤–Є–і–∞ y=ax2+bx+c. –£—Б—В–∞–љ–Њ–≤–Є—В–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–µ –Љ–µ–ґ–і—Г –Ј–љ–∞–Ї–∞–Љ–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ a –Є c –Є –≥—А–∞—Д–Є–Ї–∞–Љ–Є —Д—Г–љ–Ї—Ж–Є–є.
–Ъ–Ю–≠–§–§–Ш–¶–Ш–Х–Э–Ґ–Ђ
–Р) a>0, c<0
–С) a>0, c>0
–Т) a<0, c>0
–У–†–Р–§–Ш–Ъ–Ш
1)  2)
2)  3)
3) 
–Т —В–∞–±–ї–Є—Ж–µ –њ–Њ–і –Ї–∞–ґ–і–Њ–є –±—Г–Ї–≤–Њ–є —Г–Ї–∞–ґ–Є—В–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–є –љ–Њ–Љ–µ—А.
–Э–∞–є–і–Є—В–µ –≤—Б–µ –Ј–љ–∞—З–µ–љ–Є—П k, –њ—А–Є –Ї–∞–ґ–і–Њ–Љ –Є–Ј –Ї–Њ—В–Њ—А—Л—Е –њ—А—П–Љ–∞—П y=kx –Є–Љ–µ–µ—В —Б –≥—А–∞—Д–Є–Ї–Њ–Љ —Д—Г–љ–Ї—Ж–Є–Є y=x2+4 —А–Њ–≤–љ–Њ –Њ–і–љ—Г –Њ–±—Й—Г—О —В–Њ—З–Ї—Г. –Я–Њ—Б—В—А–Њ–є—В–µ —Н—В–Њ—В –≥—А–∞—Д–Є–Ї –Є –≤—Б–µ —В–∞–Ї–Є–µ –њ—А—П–Љ—Л–µ.
–Э–∞ —А–Є—Б—Г–љ–Ї–∞—Е –Є–Ј–Њ–±—А–∞–ґ–µ–љ—Л –≥—А–∞—Д–Є–Ї–Є —Д—Г–љ–Ї—Ж–Є–є –≤–Є–і–∞ y=kx+b. –£—Б—В–∞–љ–Њ–≤–Є—В–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–µ –Љ–µ–ґ–і—Г –≥—А–∞—Д–Є–Ї–∞–Љ–Є —Д—Г–љ–Ї—Ж–Є–є –Є –Ј–љ–∞–Ї–∞–Љ–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ k –Є b.
–У–†–Р–§–Ш–Ъ–Ш
–Р)  –С)
–С)  –Т)
–Т) 
–Ъ–Ю–≠–§–§–Ш–¶–Ш–Х–Э–Ґ–Ђ
1) k<0, b<0
2) k>0, b>0
3) k>0, b<0
–Т —В–∞–±–ї–Є—Ж–µ –њ–Њ–і –Ї–∞–ґ–і–Њ–є –±—Г–Ї–≤–Њ–є —Г–Ї–∞–ґ–Є—В–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–є –љ–Њ–Љ–µ—А.
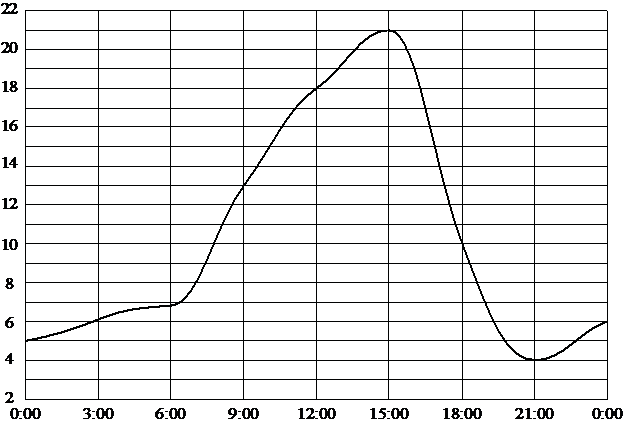 –Э–∞ —А–Є—Б—Г–љ–Ї–µ –њ–Њ–Ї–∞–Ј–∞–љ–Њ, –Ї–∞–Ї –Є–Ј–Љ–µ–љ—П–ї–∞—Б—М —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –љ–∞ –њ—А–Њ—В—П–ґ–µ–љ–Є–Є –Њ–і–љ–Є—Е —Б—Г—В–Њ–Ї. –Я–Њ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї–Є —Г–Ї–∞–Ј–∞–љ–Њ –≤—А–µ–Љ—П —Б—Г—В–Њ–Ї, –њ–Њ –≤–µ—А—В–Є–Ї–∞–ї–Є вАУ –Ј–љ–∞—З–µ–љ–Є–µ —В–µ–Љ–њ–µ—А–∞—В—Г—А—Л –≤ –≥—А–∞–і—Г—Б–∞—Е –¶–µ–ї—М—Б–Є—П. –°–Ї–Њ–ї—М–Ї–Њ —З–∞—Б–Њ–≤ –≤–Њ –≤—В–Њ—А–Њ–є –њ–Њ–ї–Њ–≤–Є–љ–µ —Б—Г—В–Њ–Ї —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –њ—А–µ–≤—Л—И–∞–ї–∞ 10¬∞C?
–Э–∞ —А–Є—Б—Г–љ–Ї–µ –њ–Њ–Ї–∞–Ј–∞–љ–Њ, –Ї–∞–Ї –Є–Ј–Љ–µ–љ—П–ї–∞—Б—М —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –љ–∞ –њ—А–Њ—В—П–ґ–µ–љ–Є–Є –Њ–і–љ–Є—Е —Б—Г—В–Њ–Ї. –Я–Њ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї–Є —Г–Ї–∞–Ј–∞–љ–Њ –≤—А–µ–Љ—П —Б—Г—В–Њ–Ї, –њ–Њ –≤–µ—А—В–Є–Ї–∞–ї–Є вАУ –Ј–љ–∞—З–µ–љ–Є–µ —В–µ–Љ–њ–µ—А–∞—В—Г—А—Л –≤ –≥—А–∞–і—Г—Б–∞—Е –¶–µ–ї—М—Б–Є—П. –°–Ї–Њ–ї—М–Ї–Њ —З–∞—Б–Њ–≤ –≤–Њ –≤—В–Њ—А–Њ–є –њ–Њ–ї–Њ–≤–Є–љ–µ —Б—Г—В–Њ–Ї —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –њ—А–µ–≤—Л—И–∞–ї–∞ 10¬∞C?
–Я–Њ—Б—В—А–Њ–є—В–µ –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є
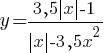
–Ю–њ—А–µ–і–µ–ї–Є—В–µ, –њ—А–Є –Ї–∞–Ї–Є—Е –Ј–љ–∞—З–µ–љ–Є—П—Е k –њ—А—П–Љ–∞—П y=kx –љ–µ –Є–Љ–µ–µ—В —Б –≥—А–∞—Д–Є–Ї–Њ–Љ –Њ–±—Й–Є—Е —В–Њ—З–µ–Ї.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: