
Постройте график функции y=x2-4|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
 x2-4x+2x, при x≥0
x2-4x+2x, при x≥0
x2-4(-x)+2x, при x<0
 x2-2x, при x≥0
x2-2x, при x≥0
x2+6x, при x<0
Рассмотрим и построим график для каждой подфункции и объединим их.
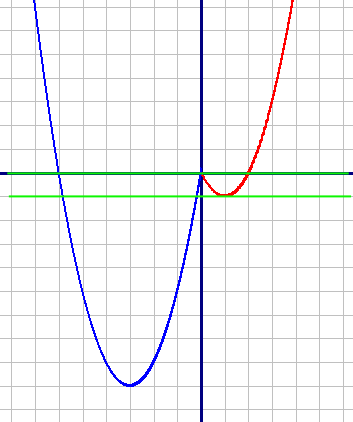 1) y1=x2-2x, при x≥0 (красный график)
1) y1=x2-2x, при x≥0 (красный график)
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -1 | 0 | 3 |
| X | 0 | -1 | -2 | -3 | -4 | -5 |
| Y | 0 | -5 | -8 | -9 | -8 | -5 |
Поделитесь решением
Присоединяйтесь к нам...
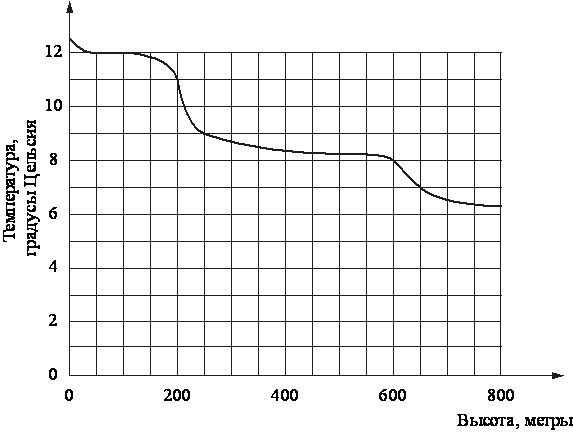 На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря.
На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря.
Определите по графику, на сколько градусов Цельсия температура на высоте 200 метров выше, чем на высоте 650 метров.
Постройте график функции
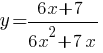
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Известно, что графики функций y=-x2+p и y=-4x+5 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
A) 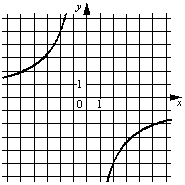 Б)
Б) 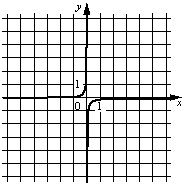 В)
В) 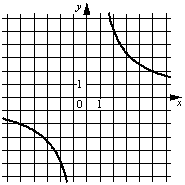
ФОРМУЛЫ
1) y=-10/x
2) y=-1/(10x)
3) y=10/x
В таблице под каждой буквой укажите соответствующий номер.
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
А) k<0, b<0 Б) k<0, b>0 В) k>0, b<0 |
1)  |
2)  |
|
3)  |
4)  |
Комментарии: