Постройте график функции y=2x+6|x|-x2 и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
y=2x+6x-x2, при x≥0
y=2x+6(-x)-x2, при x<0
8x-x2, при x≥0
y=-4x-x2, при x<0
Исследуем каждую подфункцию:
1) y=8x-x2
Это квадратичная функция, следовательно график - парабола. Коэффициент а=-1 (т.е. меньше нуля), следовательно ветви параболы направлены вниз. Найдем точки пересечения графика с осью Х, для этого решим уравнение 8x-x2=0
x(8-x)=0
x1=0
x2=8
2) y=-4x-x2
Это квадратичная функция, следовательно график - парабола. Коэффициент а=-1 (т.е. меньше нуля), следовательно ветви параболы направлены вниз. Найдем точки пересечения графика с осью Х, для этого решим уравнение -4x-x2=0
x(-4-x)=0
x1=0
x2=-4
Построим график для каждой подфункции и объединим их.
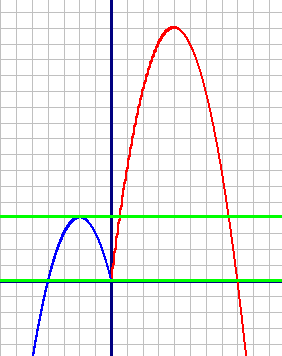1) y1=8x-x2, при x≥0 (красный график)
| X | 0 | 2 | 4 | 6 |
| Y | 0 | 12 | 16 | 12 |
| X | 0 | -1 | -2 | -3 | -4 |
| Y | 0 | 3 | 4 | 3 | 0 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции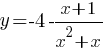 
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
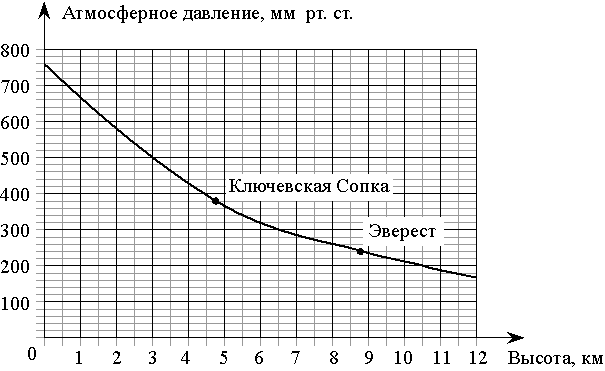На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Ключевской Сопки?
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Большого Шелома?
Постройте график функции
-x2, если |x|≤1
1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
Постройте график функции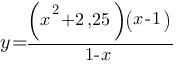 
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-11-28 20:38:12) Администратор: Елена, а по-русски?
(2016-11-28 14:13:28) Елена : Описати перетворення f(x)=(x-3^2-2