
Решение какого из данных неравенств изображено на рисунке?

1) x2-7x<0
2) x2-49>0
3) x2-7x>0
4) x2-49<0
Посмотрим на предложенные неравенства:
- все они квадратичные, т.е. графики этих функций - параболы
- у всех аргумент "а" равен единице, т.е. больше нуля, следовательно ветви их парабол направлены вверх
- графики парабол 1) и 3) будут совпадать, т.к. это одинаковые функции.
- графики парабол 2) и 4) будут совпадать, т.к. это одинаковые функции.
Посмотрим на рисунок решения неравенства:
- корни квадратичной функции должны быть 0 и 7.
 Решим уравнение x2-7x=0
Решим уравнение x2-7x=0
x(x-7)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому:
1) x1=0
2) x-7=0 => x2=7
Посмотрим на рисунок, в условии показаны диапазоны, когда график функции выше оси Х, т.е. больше нуля, следовательно, подходит неравенство x2-7x>0
Проверим уравнение x2-49=0
x2-72=0
(x-7)(x+7)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому:
1) x-7=0 => x1=7
2) x+7=0 => x2=-7
Корни не совпали с указанными на рисунке, следовательно неравенства x2-49 не подходят.
Ответ: 3)
Поделитесь решением
Присоединяйтесь к нам...
Решите систему уравнений 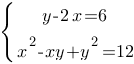
Решите систему неравенств 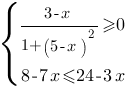
Товар на распродаже уценили на 20%, при этом он стал стоить 940 р. Сколько рублей стоил товар до распродажи?
На счёт в банке, доход по которому составляет 20% годовых, внесли 29 тыс. руб.. Сколько тысяч рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?
На каком рисунке изображено множество решений неравенства
3-4x>11-8(x-2)?
1) 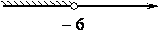
2) 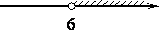
3) 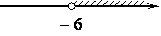
4) 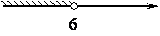
Комментарии: