
Решите систему неравенств 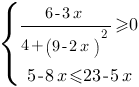
Чтобы решить систему неравенств, необходимо решить каждое неравенство по отдельности и пересечь полученные диапазоны. Диапазон, полученный в результате пересечения и будет решением системы неравенств.
Решаем первое неравенство:
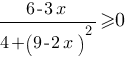
Запишем Область Допустимых Значений (ОДЗ):
Так как на ноль делить нельзя, то 4+(9-2x)2 не может равняться нулю. Найдем недопустимые значения X, для этого можно решить квадратное уравнение 4+(9-2x)2=0 через
дискриминант и найти корни, а так же можно заметить, что:
(9-2x)2=-4
Т.е. квадрат равен отрицательному числу, чего быть не может.
Следовательно, данное уравнение не имеет решений.
Т.е. значения X ничем не ограничено, переходим к решению.
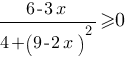
Опять посмотрим внимательно на эту дробь:
Знаменатель всегда положительный, так как положительное число плюс квадрат числа всегда дадут положительный результат.
Получается, что данная дробь будет больше или равна нулю, когда числитель больше или равен нулю:
6-3x≥0
6≥3x
2≥x
Решаем второе неравенство:
5-8x≤23-5x
5-23≤8x-5x
-18≤3x
-6≤x

Накладиваем диапазоны на одну ось:

Зеленым цветом отмечено пересечение диапазонов [-6;2]
Ответ: [-6;2]
Поделитесь решением
Присоединяйтесь к нам...
Решите систему неравенств 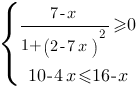
Найдите наибольшее значение x, удовлетворяющее системе неравенств
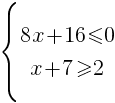
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 57 км/ч, а вторую половину пути проехал со скоростью на 38 км/ч больше скорости первого, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.
После уценки телевизора его новая цена составила 0,99 старой. На сколько процентов уменьшилась цена телевизора в результате уценки?
Какое из приведённых ниже неравенств является верным при любых значениях a и b, удовлетворяющих условию a<b?
1) a-b>5
2) b-a>3
3) a-b<3
4) b-a<1
Комментарии: