Решите неравенство 
Первое: это неравенство ни при каких х не будет равно нулю, так как чтобы дробь была равна нулю, числитель должен быть равен нулю, а у нас он равен 19.
Значит мы можем превратить это нестрогое неравенство в строгое, ничего при этом не теряя:
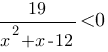
Второе: данная дробь будет меньше нуля, только когда знаменатель будет меньше нуля (так как числитель положительный). Причем знаменатель строго больше нуля, так как он не может быть равен нулю (на ноль делить нельзя).
Получаем неравенство: x2+x-12<0
Найдем корни квадратного уравнения x2+x-12=0
D=12-4*1*(-12)=1+48=49
x1=(-1+7)/2=3
x2=(-1-7)/2=-4
График этой квадратичной функции - парабола. Ветви параболы направлены вверх, т.к. коэффициент "а" равен 1 (т.е. больше нуля).
Нас интересуют диапазон, где эта функция меньше нуля, т.е. располагается под осью Х:
(-4;3)
Ответ: (-4;3)
Поделитесь решением
Присоединяйтесь к нам...
Укажите решение неравенства 3x-2(x-5)≤-6.
1) [4;+∞)
2) (-∞;4]
3) (-∞;-16]
4) [-16;+∞)
На координатной прямой отмечено число c. Расположите в порядке убывания числа c, c2 и 1/c.
Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 2 часа, вернулись обратно через 6 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 6 км/ч?
Решите уравнение -3x2+4x-7=-x2+5x-(-1+2x2).
На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя?
Хочу получать новые решения
Ни какого спама
Автор: Таська
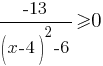
Комментарии: