Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 2 часа, вернулись обратно через 6 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 6 км/ч?
Обозначим:
S - расстояние от лагеря до места прогулки.
t1 - время движения лодки против течения.
t2 - время движения лодки по течению.
Скорость лодки против течения равна 6-3=3 км/ч, по течению - 6+3=9 км/ч.
Составим уравнения:
движение лодки против течения:
S=3t1
движение лодки по течению:
S=9t2
время в поездке:
6=t1+t2+2
t1=4-t2
S=3(4-t2)
S=9t2
Вычтем из первого уравнения второе:
S-S=3(4-t2)-9t2
0=12-3t2-9t2
0=12-12t2
t2=1
Подставляем во второе уравнение:
S=9t2=9*1=9 км.
Ответ: 9 км.
Поделитесь решением
Присоединяйтесь к нам...
На каком рисунке изображено множество решений системы неравенств
х+2,7≤0,
х+4≥1?
1) 
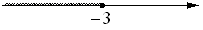
2) 
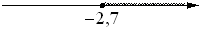
3) 
4) 
Решите уравнение 5x2=35x.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
На координатной прямой отмечено число a.
Расположите в порядке возрастания числа a-1, 1/a, a.
1) a, 1/a , a-1
2) a, a-1, 1/a
3) a-1, a, 1/a
4) 1/a, a-1, a
Решите систему неравенств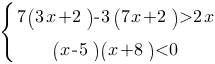 
Решите уравнение 1-5x=-6x+8.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: