
Из пунктов А и В, расстояние между которыми 27 км, вышли одновременно навстречу друг другу два туриста и встретились в 12 км от В. Турист, шедший из А, сделал в пути получасовую остановку. Найдите скорость туриста, шедшего из В, если известно, что он шёл со скоростью, на 2 км/ч меньшей, чем первый турист.
Введем обозначения:
va - скорость туриста, вышедшего из пункта A;
ta - время в пути туриста, вышедшего из пункта A;
vb - скорость туриста, вышедшего из пункта B;
tb - время в пути туриста, вышедшего из пункта B;
Из условия задачи известно, что:
va=vb+2;
ta=tb-0,5 (т.к. турист А непосредственно шел на пол часа меньше, чем турист В)
Турист А прошел 27-12=15 км,
а турист В прошел 12 км.
Тогда получаем систему:
 15=vata
15=vata
12=vbtb
 15=(vb+2)(tb-0,5)
15=(vb+2)(tb-0,5)
12=vbtb
 15=vbtb-0,5vb+2tb-1
15=vbtb-0,5vb+2tb-1
12=vbtb
 16=vbtb-0,5vb+2tb
16=vbtb-0,5vb+2tb
12/vb=tb
 16=vb12/vb-0,5vb+2*12/vb
16=vb12/vb-0,5vb+2*12/vb
12/vb=tb
 16=12-0,5vb+24/vb
16=12-0,5vb+24/vb
12/vb=tb
 4=-0,5vb+24/vb
4=-0,5vb+24/vb
12/vb=tb
 4vb=-0,5vb2+24
4vb=-0,5vb2+24
12/vb=tb
 8vb=-vb2+48
8vb=-vb2+48
12/vb=tb
 vb2+8vb-48=0
vb2+8vb-48=0
12/vb=tb
Решим квадратное уравнение:
D=82-4*1*(-48)=64+192=256
vb1=(-8+16)/(2*1)=4
vb2=(-8-16)/(2*1)=-12
Так как скорость отрицательной быть не может, то vb=4 км/ч
Ответ: vb=4 км/ч
Поделитесь решением
Присоединяйтесь к нам...
Стоимость проезда в электропоезде составляет 119 рублей. Школьникам предоставляется скидка 50%. Сколько рублей будет стоить проезд для 5 взрослых и 28 школьников?
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 70 человек. Голоса между кандидатами распределились в отношении 3:7. Сколько голосов получил победитель?
Решите систему уравнений 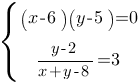
Решите уравнение (x+2)(-x+6)=0.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Решите уравнение x3+5x2-9x-45=0.
Комментарии: