Постройте график функции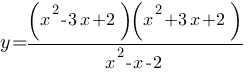 
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Запишем Область Допустимых Значений (ОДЗ).
Так как на ноль делить нельзя, то x2-x-2≠0
Найдем такие х, для этого
решим
квадратное уравнение x2-x-2=0
D=(-1)2-4*1*(-2)=1+8=9
x1=(-(-1)+3)/(2*1)=4/2=2
x2=(-(-1)-3)/(2*1)=-2/2=-1
Правильно будет написать, что x≠2 и x≠-1
Упростим данную функцию, для этого разложим все 3 квадратных уравнения на множители. Каждое квадратное уравнение (если у него есть корни) можно представить в виде (x-x1)(x-x2), где x1 и x2 - корни этого уравнения.
Знаменатель мы уже сейчас можем разложить на множители:
x2-x-2=(x-2)(x-(-1))=(x-2)(x+1)
Разложим x2-3x+2
D=(-3)2-4*1*2=9-8=1
x1=(-(-3)+1)/(2*1)=4/2=2
x2=(-(-3)-1)/(2*1)=2/2=1
Получаем:
x2-3x+2=(x-2)(x-1)
Разложим x2+3x+2
D=32-4*1*2=9-8=1
x1=(-3+1)/(2*1)=-2/2=-1
x2=(-3-1)/(2*1)=-4/2=-2
x2+3x+2=(x-(-1))(x-(-2))=(x+1)(x+2)
В итоге получаем:
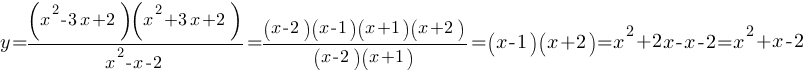
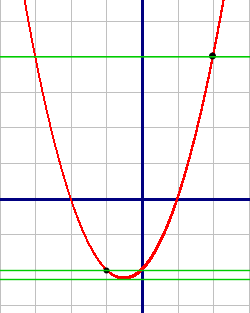Построим график (красный) этой функции по точкам:
| X | -3 | -2 | -1 | 0 | 1 | 2 |
| Y | 4 | 0 | -2 | -2 | 0 | 4 |
Поделитесь решением
Присоединяйтесь к нам...
На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику,
через сколько минут с момента запуска двигатель нагреется до 40°C.
Постройте график функции
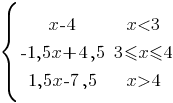
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции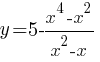 
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
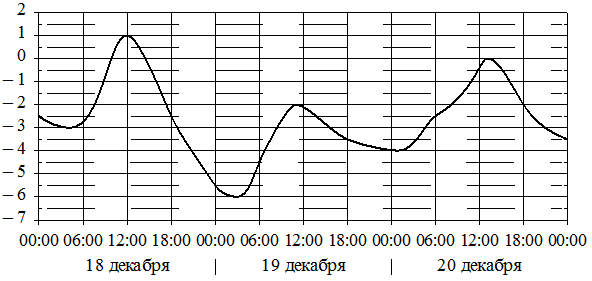На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 19 декабря. Ответ дайте в градусах Цельсия.
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) y=-2x+4
Б) y=2x-4
В) y=2x+4
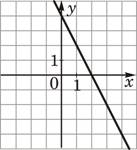
ГРАФИКИ
1) 
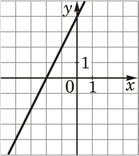2) 
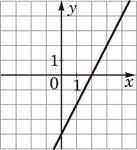3) 
В таблице под каждой буквой укажите соответствующий номер.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: