ОГЭ, Математика.
Функции: Задача №7493BA

Задача №266 из 287
Условие задачи:

Постройте график функции

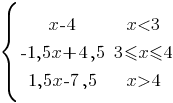
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.

Решение задачи:

Построим графики всех трех подфункций на определенным им диапазонах.
Первая подфункция:
y₁=x-4, при x<3.
График функции представляет из себя прямую.
Вторая подфункция:
y₂=-1,5x+4,5, при 3≤x≤4 - прямая.
Третья подфункция:
y₃=1,5x-7,5, при x>4 - тоже прямая.
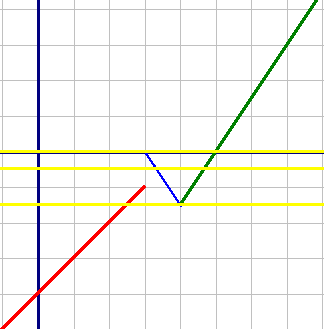Построим все три графика по точкам:
y₁=x-4, если x<3 (красный).

X	0	1	2
Y	-4	-3	-2

y₂=-1,5x+4,5, если 3≤x≤4 (синий).

X	3	4
Y	0	-1,5

y₃=1,5x-7,5, если x>4 (зеленый).

X	4	5	6
Y	-1,5	0	1,5

Желтым цветом построены прямы y=m, которые имеют с графиком ровно две общие точки.
Если проводить горизонтальную прямую y=m снизу вверх, то две общие точки будут:
1) когда прямая проходит через излом между синей и зеленой подфункциями, т.е. m=-1,5.
2) когда прямая становится выше красной прямой, но не выше синей, т.е. m∈(-1;0].
Ответ: m∈-1,5∪(-1;0]

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №9F911C

Постройте график функции y=x²-6|x|-2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.

Задача №071A69

На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А) Б) В)
КОЭФФИЦИЕНТЫ
1) k<0, b>0 2) k<0, b<0 3) k>0, b>0
В таблице под каждой буквой укажите соответствующий номер.

Задача №E7EF61

Постройте график функции y=|x²-x-2|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?

Задача №2BA3BA

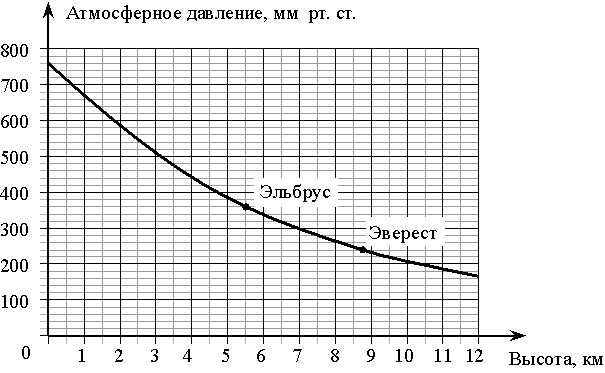На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Эльбруса?