
Постройте график функции y=(x2+6,25)(x-1)/(1-x) и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Построим график функции:
y=(x2+6,25)(x-1)/(1-x)
Область Допустимых Значений (ОДЗ):
(1-x) не может быть равно нулю, т.к. делить на ноль нельзя. Следовательно, x≠1
y=(x2+6,25)(x-1)/(1-x)
y=(x2+6,25)(-1)(1-x)/(1-x)
y=-(x2+6,25)
y=-x2-6,25
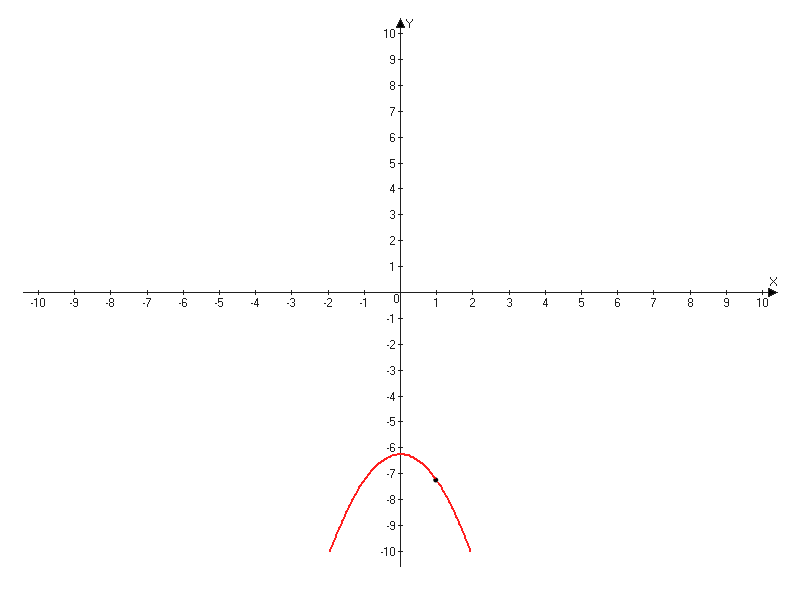
Две функции имеют точку пересечения, это означает, что графики обеих функций имеют общую точку. Следовательно, надо составить систему и решить ее:
 y=-x2-6,25
y=-x2-6,25
y=kx
kx=-x2-6,25
x2+kx+6,25=0
Решим это
квадратное уравнение:
D=k2-4*1*6,25=k2-25
В условии сказано, что точка пересечения только одна, следовательно корень уравнения должен быть только один. Это условие выполняется, когда дискриминант равен нулю:
D=k2-25=0
k2=25
k1=5
k2=-5
 Заметим, что в графике имеется "выколотая" точка, значит прямая y=kx, проходя через эту выколотую точку, пересечется с графиком один раз в другой точке, ниже по графику.
Заметим, что в графике имеется "выколотая" точка, значит прямая y=kx, проходя через эту выколотую точку, пересечется с графиком один раз в другой точке, ниже по графику.
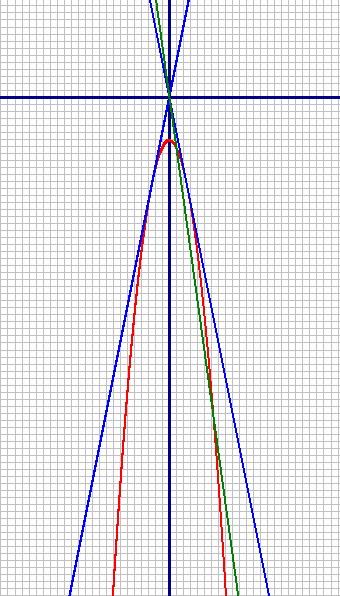
Для наглядности уменьшим масштаб графика параболы:
Красным цветом начерчена парабола y=-x2-6,25
Синим цветом начерчены прямые y=5x и y=-5x.
Зеленым цветом проведена прямая через начало координат и выколотую точку. Как видно, она тоже имеет только одну общую точку с параболой.
Координата х известна из ОДЗ х=1.
Найдем координату y "выколотой" точки. y(1)=-12-6,25=-7,25
Подставляем эти координаты в уравнение прямой y=kx:
-7,25=k*1 => k=-7,25
Ответ: k1=5, k2=-5, k3=-7,25
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
 x2, если |x|≤1
x2, если |x|≤1
1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
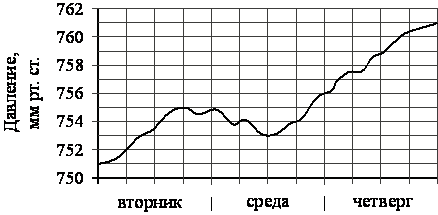 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления в среду (мм рт. ст.).
На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления в среду (мм рт. ст.).
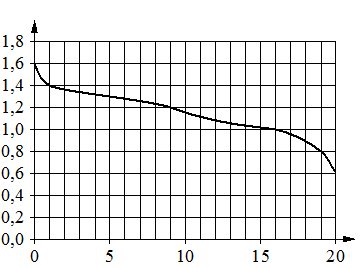 При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,6 В до 1 В.
При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,6 В до 1 В.
На рисунке изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) a>0, c<0 2) a<0, c<0 3) a>0, c>0 4) a<0, c>0 |
А)  |
Б)  |
В)  |
Постройте график функции y=|x|x+|x|-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Комментарии:
(2017-02-19 01:15:33) Администратор: Руслан, я добавил в решение рисунок, думаю так стало понятней.
(2017-02-18 23:52:07) Руслан: Действительно, причем здесь выколотая точка? Там же нет пораболы, знчит, там не можетпересекаться с прямой.
(2017-02-17 17:10:44) : При чём тут выколотая точка
(2015-04-09 14:42:27) Администратор: y=-(x2+6,25), -1 стал минусом перед скобкой (x2+6,25).
(2015-04-09 14:39:55) : y=(x2+6,25)(-1)(1-x)/(1-x) откуда здесь -1?
(2014-05-30 09:24:33) Администратор: Евгений, как Вы получили число -5,25?
(2014-05-30 07:39:08) Евгений : при к=-5,25 прямая у=кх тоже будет иметь одну общую точку, с параболой?!
(2014-05-27 15:11:28) Администратор: Евгений, а почему Вы так решили?
(2014-05-27 10:24:29) Евгений : при к=-5,25 прямая у=кх тоже будет иметь одну общую точку, с параболой?!
(2014-05-27 08:02:01) Евгений : при к=-5,25 прямая у=кх тоже будет иметь одну общую точку, с параболой?!