ЕГЭ, Математика (базовый уровень).
Уравнения и неравенства: Задача №4B3BFE

Решите уравнение x²+8=6x.
Если уравнение имеет более одного корня, в ответе укажите больший из них.

Другие задачи из этого раздела

Задача №DE39F4

Среди дачников в посёлке есть те, кто выращивает виноград, и есть те, кто выращивает груши. А также есть те, кто не выращивает ни виноград, ни груши. Некоторые дачники в этом посёлке, выращивающие виноград, также выращивают и груши. Выберите утверждения, которые верны при указанных условиях.
1) Если дачник из этого посёлка не выращивает виноград, то он выращивает груши.
2) Среди тех, кто выращивает виноград, есть дачники из этого посёлка.
3) Есть хотя бы один дачник в этом посёлке, который выращивает и груши, и виноград.
4) Если дачник в этом посёлке выращивает виноград, то он не выращивает груши.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Задача №694B19

На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 9 кусков, если по жёлтым — 12 кусков, а если по зелёным — 8 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?

Задача №757449

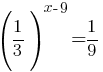
Решите уравнение x²=-2x+24.
Если уравнение имеет более одного корня, в ответе укажите больший из них.

Задача №FD1E47

Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

Задача №27524E

Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны при приведённом условии.
1) Если Шарик не лает, значит, по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять. В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.