Решите уравнение x2-6x+√
x2-6x+√
Обозначим Область Допустимых Значений (ОДЗ).
Значение под корнем не может быть отрицательным, следовательно:
6-x≥0
6≥x
x2-6x+√
x2-6x-7=0
Решим это
квадратное уравнение через
дискриминант:
D=(-6)2-4*1*(-7)=36+28=64
x1=(-(-6)+8)/(2*1)=(6+8)/2=7
x2=(-(-6)-8)/(2*1)=(6-8)/2=-1
Накладываем на решение ОДЗ, подходит только x2=-1
Ответ: -1
Поделитесь решением
Присоединяйтесь к нам...
Найдите ƒ(3), если ƒ(x-1)=76-x
Найдите значение выражения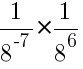 
В какое из следующих выражений можно преобразовать дробь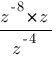 
?
1) z-3
2) z-11
3) z3
4) z-1
Какое из данных ниже чисел является значением выражения 212*(23)-5?
1) 8
2) 1024
3) -8
4) 1/8
Какое из данных ниже чисел является значением выражения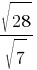 
?
1) 2
2) 2√7
3) 14
4) 4√7
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-09-29 16:35:47) Администратор: Леха, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2019-09-26 12:12:44) Леха: Все под корнем до знака больше или равно √x²+5<=|x+2|