
Решите уравнение (x2-36)2+(x2+4x-12)2=0.
(x2-36)2+(x2+4x-12)2=0
(x2-62)2+(x2+4x-12)2=0
(
(x-6)(x+6))2+(x2+4x-12)2=0
(x-6)2(x+6)2+(x2+4x-12)2=0
Разложим на множители x2+4x-12:
x2+4x-12=(x-x1)(x-x2), где x1 и x2 - корни уравнения x2+4x-12=0
Найдем корни:
D=42-4*1*(-12)=16+48=64
x1=(-4+8)/(2*1)=4/2=2
x2=(-4-8)/(2*1)=-12/2=-6
x2+4x-12=(x-2)(x-(-6))=(x-2)(x+6)
Подставляем в первоначальное уравнение:
(x-6)2(x+6)2+((x-2)(x+6))2=0
(x-6)2(x+6)2+(x-2)2(x+6)2=0
Выносим (x+6)2 за скобки:
(x+6)2((x-6)2+(x-2)2)=0
Произведение равно нулю, когда один из множителей равен нулю:
1) (x+6)2=0
x1=-6
2) (x-6)2+(x-2)2=0
(x-6)2=-(x-2)2
Так как квадрат числа всегда больше или равен нулю, то
 x-6=0
x-6=0
x-2=0
Такая система не имеет решений.
Ответ: x=-6
Поделитесь решением
Присоединяйтесь к нам...
Укажите решение неравенства -3-x≥4x+7.
1) (-∞; -0,8)
2) (-∞; -2)
3) (-2; +∞)
4) (-0,8; +∞)
Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 30 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
Поезд, двигаясь равномерно со скоростью 135 км/ч, проезжает мимо столба за 4 секунды. Найдите длину поезда в метрах.
Укажите решение системы неравенств
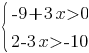
1) нет решений
2) 
3) 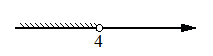
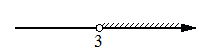
4) 
Решите уравнение -2x2+x+7=-x2+5x+(-2-x2).
Комментарии:
(2015-03-24 08:33:54) дмитрий: Спасибо!