
При каких отрицательных значениях k прямая y=kx-4 имеет с параболой y=x2+2x ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
Чтобы найти точки пересечения функций необходимо составить систему из этих функций и решить ее. Решением системы будут координаты точек пересечения
 y=kx-4
y=kx-4
y=x2+2x
kx-4=x2+2x
0=x2+2x-kx+4
0=x2+x(2-k)+4
Решим это квадратное уравнение:
D=(2-k)2-4*1*4=(2-k)2-16
В условии задачи сказано, что точка пересечения должна быть только одна, следовательно система должна иметь только одно решение, значит квадратное уравнение должно иметь только один корень. Следовательно, дискриминант нужно приравнять к нулю (только тогда будет только один корень):
D=(2-k)2-16=0
(2-k)2-42=0
Применим формулу
разность квадратов:
((2-k)-4)((2-k)+4)=0
(2-k-4)(2-k+4)=0
(-k-2)(-k+6)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) -k-2=0
k1=-2
2) -k+6=0
k2=6
По условию задачи нас интересует только отрицательное k, следовательно k=-2.
Т.е. уравнение прямой выглядит так:
y=-2x-4
Продолжим искать точку пересечения графиков, вернемся к уравнению:
0=x2+x(2-k)+4
0=x2+x(2-(-2))+4
0=x2+4x+4
D=0 (так как точка пересечения только одна, следовательно корень уравнения тоже должен быть только один)
x=-4/2=-2
Подставляем в любую функцию (результат будет один и тот же), но для простоты подставим в уравнение прямой:
y=-2x-4=-2(-2)-4=4-4=0
(-2; 0) - точка пересечения графиков.
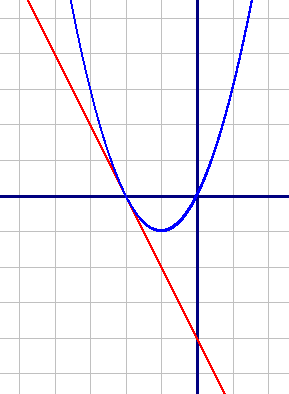 Построим графики функций по точкам:
Построим графики функций по точкам:
y=-2x-4 (красный график)
| X | -2 | -1 | 0 |
| Y | 0 | -2 | -4 |
| X | -3 | -2 | -1 | 0 |
| Y | 3 | 0 | -1 | 0 |
Поделитесь решением
Присоединяйтесь к нам...
Одно из чисел √40, √46, √53, √58 отмечено на прямой точкой A.
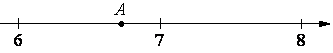
Какое это число?
1) √40
2) √46
3) √53
4) √58
На координатной прямой отмечены числа а и с.

Какое из следующих утверждений неверно?
1) a-c>0
2) -3<a+1<-2
3) a/c<0
4) -c>-1
Одно из чисел 4/7; 6/7; 8/7; 13/7 отмечено на прямой точкой.
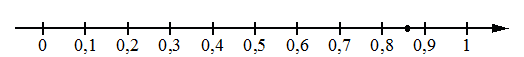
Какое это число?
1) 4/7
2) 6/7
3) 8/7
4) 13/7
Какому из следующих чисел соответствует точка, отмеченная на координатной прямой?

1) 6/23
2) 9/23
3) 10/23
4) 11/23
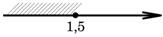
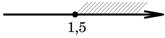
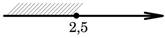
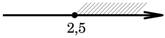
На каком рисунке изображено множество решений неравенства 2+x≤5x-8?
1) 
2) 
3) 
4) 
Комментарии: