Решение какого из данных неравенств изображено на рисунке?
1) x2-36<0
2) x2-6x<0
3) x2-6x>0
4) x2-36>0
Посмотрим на предложенные неравенства:
- все они квадратичные, т.е. графики этих функций - параболы
- у всех аргумент "а" равен единице, т.е. больше нуля, следовательно ветви их парабол направлены вверх
- графики парабол 1) и 4) будут совпадать, т.к. это одинаковые функции.
- графики парабол 2) и 3) будут совпадать, т.к. это одинаковые функции.
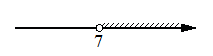
Посмотрим на рисунок решения неравенства:
- корни квадратичной функции должны быть 0 и 6.
Решим уравнение x2-36=0
x2-62=0
(x-6)(x+6)=0
x-6=0 => x1=6
x+6=0 => x2=-6
Неравенства 1) и 4) не подходят.
Решим уравнение x2-6x=0
x(x-6)=0
Произведение равно нулю, когда один из множителей равен нулю, получаем:
x1=0
x-6=0 => x2=6
Значит неравенства 2) и 3) подходят (судя по корням).
Посмотрим на рисунок, в условии показан диапазон, когда график функции ниже оси Х, т.е. меньше нуля, следовательно, подходит неравенство x2-6x<0
Ответ: 2)
Поделитесь решением
Присоединяйтесь к нам...
Решите систему неравенств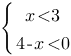 
На каком рисунке изображено множество её решений?
1) 
2) Система не имеет решений
3) 
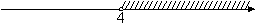
4) 
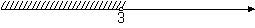
На координатной прямой отмечено число a.
Из следующих утверждений выберите верное.
1) (a-6)2>1
2) (a-7)2<1
3) a2<36
4) a2>49
Укажите решение системы неравенств
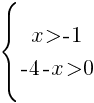
1) 
2) 
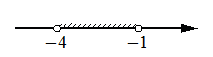
3) 
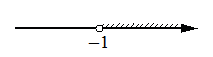
4) система не имеет решений
При каких положительных значениях k прямая y=kx-4 имеет с параболой y=x2-3x ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
Укажите решение системы неравенств
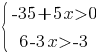
1) 
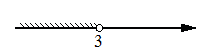
2) 
3) нет решений
4) 
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: