Какое наибольшее число последовательных натуральных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма была меньше 465?
Иными словами, 1+2+3+4+...+n<465. Чему равен максимальный n?
Это
арифметическая прогрессия, разность прогрессии d=1, используем
формулу суммы:
Sn=(2*1+(n-1)*1)*n/2
Эта сумма должна быть меньше 465.
(2*1+(n-1)*1)*n/2<465
(2+n-1)n<930
n2+n-930<0
Решим это неравенство,
решив сначала уравнение n2+n-930=0
D=12-4*1*(-930)=1+3720=3721
n1=(-1+61)/(2*1)=60/2=30
n2=(-1-61)/(2*1)=-62/2=-31
Т.е. n∈(-31;30), заметьте крайние точки не включаются.
nmax=29
Ответ: 29
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции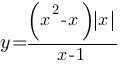 
. Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Найдите f(2), если f(x-4)=68-x.
Постройте график функции y=|x|(x-1)-3x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Найдите значение выражения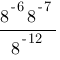 
1) -1/8
2) -8
3) 8
4) 1/8
Решите уравнение (x-3)(x-4)(x-5)=(x-2)(x-4)(x-5).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: